Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 93

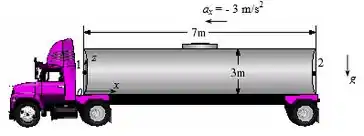
Um tanque cilíndrico com 3   m de diâmetro e 7   m de comprimento é preenchido completamente com água. O tanque é puxado por um caminhão em uma estrada nivelada com eixo de 7   m de comprimento na horizontal. Determine a diferença de pressão entre a parte dianteira e traseira do tanque ao longo de uma reta horizontal quando o caminhão ( a ) acelera a 3   m / s 2 e ( b ) desacelera a 4   m / s 2 .

Passo 1

Fala aí galera, bora fazer mais uma questão de MecFlu. Primeiramente, a aceleração horizontal está na direção x negativa e, portanto, a x é negativo. Além disso, não há aceleração na direção vertical e, portanto, a z = 0 . A diferença de pressão entre dois pontos 1 e 2 em um fluido incompressível em movimento linear rígido do corpo é dada por:

Logo:

P 2 - P 1 = - ρ a x x 2 - x 1 - ρ g + a z z 2 - z 1 P 2 - P 1 = ρ a x x 2 - x 1

Sabemos que z2 - z1 = 0 ao longo do eixo horizontal. Portanto, a diferença de pressão entre a frente e a traseira do tanque é devida à aceleração na direção horizontal e ao efeito de compressão resultante na parte traseira do tanque. Então a diferença de pressão ao longo do eixo horizontal se torna:

∆ P = P 2 - P 1 = - ρ a x x 2 - x 1 ∆ P = - 1000 k g m 3 - 3 m s 2 7   m ∆ P = 21   k P a

Passo 2

Agora, precisamos encontrar a diferença de pressão com uma aceleração de a x = 4   m / s 2 . Para isso, basta repetirmos o processo anterior. Fica assim:

∆ P = P 2 - P 1 = - ρ a x x 2 - x 1 ∆ P = - 1000 k g m 3 4   m s 2 7   m ∆ P = - 2 8   k P a

Resposta

∆ P = 21   k P a

∆ P = - 28   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A densidade de um corpo flutuante pode ser determinada ligando-se pesos ao corpo até que o corpo e os pesos estejam completamente submersos e, em seguida, pesando-os separadamente no ar. Considere uma
Um domo hemisférico de 50t o n e diâmetro de 6m sobre uma superfície nivelada é preenchida com água, como mostra a figura P 3 - 122 . Uma pessoa diz que pode elevar esse domo utilizando a lei de Pasca
Repita o Problema 3-118 para uma altura de água de 1,2m acima da dobradiça em B .
A comporta retangular de 200k g e 5m de largura mostrada na figura P 3 - 118 tem dobradiças em B e se inclina contra o piso em A , formando um ângulo de 45 ° com a horizontal. A comporta deve ser aber
A água de um reservatório com 25m de profundidade mantida no seu interior por uma parede com 150m de largura cuja seção transversal é um triângulo equilátero, como mostra a Figura P3-123. Determine (a