Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 6.Problemas - Ex. 33

Considere o c h i p sobre a placa de circuito impresso do Problema 6.31. Para assegurar uma operação confiável por longos períodos de tempo, a temperatura no chip não deve exceder 85 ° C . Supondo a disponibilidade de ar forçado a T ∞ = 25 ° C e a aplicabilidade da correlação para a transferência de calor já especificada, calcule e represente graficamente a dissipação máxima de potência permitida para o chip, P c , em função da velocidade do ar para 1 ≤ V ≤ 25   m / s . Se a superfície do chip possuir uma emissividade de 0,80 e a placa de circuito se encontrar no interior de um grande recipiente cujas paredes estejam a 25 ° C , qual é o efeito da radiação no gráfico P c – V ?

Passo 1

Começamos o nosso problema realizando algumas considerações sobre o nosso sistema:

- Estado Estacionário;

- Variação de temperatura no chip desprezíveis;

- Transferência de calor ocorrendo exclusivamente pela superfície superior do chip;

- O coeficiente de transferência de calor local em x = L fornece uma boa aproximação do coeficiente médio de transferência de calor para a superfície do chip.

Pela Tabela A.4 a temperatura média de 328   K , obtemos:

v = 18,71 × 10 - 6   m 2 / s

k = 0,0284   W / m ⋅ K

P r = 0,703

Passo 2

Agora, devemos aplicar um balanço de energia em nosso sistema:

E ˙ e n t - E ˙ s a i + E ˙ g = 0

P e = q c o n v + q r a d

Abrindo essa equação:

P e = h - A s T e - T ∞ + h r A s T e - T v i z  

Temos:

h r = ε σ T e - T v i z T e 2 + T v i z 2

Sendo:

N u L = 0,04 R e L 0,85 P r 1 3

E também podemos colocar:

N u L = h - L k

h - = 0,04 R e L 0,85 P r 1 3 k L

Substituindo na nossa equação:

P e = 0,04 R e L 0,85 P r 1 3 k L A s T e - T ∞ + h r A s T e - T v i z  

P e = l 2 0,04 R e L 0,85 P r 1 3 k L T e - T ∞ + ε σ T e - T v i z T e 2 + T v i z 2 T e - T v i z  

Passo 3

Sendo:

R e L = V L v

Temos:

P e = l 2 0,04 P r 1 3 k V 0,85 L 0,15 v 0,85 T c - T ∞ + ε σ T e - T v i z T e 2 + T v i z 2 T e - T v i z  

Substituindo os dados:

P e = 0,004 2 ⋅ 0,04 ⋅ 0,703 1 3 ⋅ 0,0284 ⋅ V 0,85 0,120 0,15 ⋅ 18,71 × 10 - 6 0,85 ⋅ 85 - 25 + ε ⋅ 5,67 × 10 - 8 ⋅ 85 - 25 ⋅ 358 2 + 298 2 ⋅ 85 - 25  

Calculando o lado direito da nossa expressão para ε = 0 e ε = 0,85 , obtemos os seguintes resultados para 1 ≤ V ≤ 25   m / s :

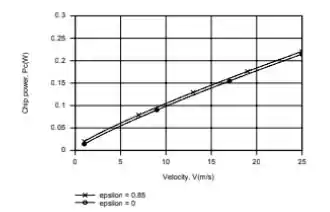
Visto que h L aumenta com V 0,85 , a potência do chip deve aumentar com V da mesma maneira. Troca de radiação aumenta o P e em um valor fixo, mas pequeno 6   m W .

Enquanto h L varia de 14,5 a 223   W / m 2 ⋅ K sobre a faixa de velocidade descrita, sendo h r = 6,5   W / m 2 ⋅ K uma constante independente de V .

Resposta

Discursiva

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra retangular com comprimento característico de 0,5 m é colocada em um fluxo livre, com coeficientes de transferência de calor por convecção de 100 W/m2.K e 50 W/m2.K quando as velocidades do f
Considere um fluido que escoa sobre uma placa plana, em velocidade constante de fluxo livre. O número crítico de Reynolds é 5 x 105, e a distância da ponta em que a transição de fluxo laminar para tur
86 – O número de ____________ é um parâmetro adimensional importante para convecção forçada, e o número de ____________ é um parâmetro adimensional importante para convecção natural. a R e y n o l d s
A transição do escoamento laminar para turbulento em situação de convecção forçada é determinada por qual dos seguintes números adimensionais?(a) Grasshof(b) Nusselt(c) Reynolds(d) Stanton(e) Mach
Ar forçado a T ∞ = 25 ° C e V = 10m / s é usado para resfriar elementos eletrônicos em uma placa de circuito. Um desses elementos é um chip, que mede 4m m por 4m m , localizado a 120m m da aresta fron