Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 8º - Capítulo 3.Problemas - Ex. 26
Considere um transistor de potência encapsulado em uma caixa de alumínio que é fixado em sua base a uma placa quadrada de alumínio de condutividade térmica , espessura e largura . A caixa é unida à placa por parafusos que mantêm uma pressão de contato de , e a superfície posterior da placa transfere calor por convecção natural e radiação para o ar ambiente e grandes arredores em . A superfície tem uma emissividade de , e o coeficiente de convecção é . A caixa é completamente fechada de forma que a transferência de calor pode ocorrer exclusivamente através da placa de base.
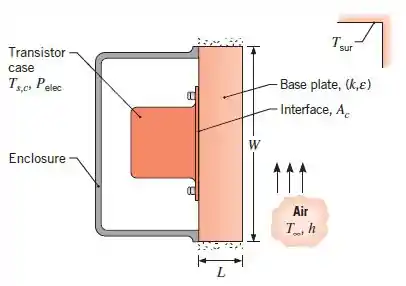
(a) Se a interface de alumínio para alumínio preenchida com ar for caracterizada por uma área de e uma rugosidade de , qual é a dissipação de potência máxima permitida se a temperatura da superfície do caso, , não deve exceder ?
(b) O coeficiente de convecção pode ser aumentado submetendo a superfície da placa a um fluxo forçado de ar. Explore o efeito de variar o coeficiente ao longo do intervalo .
Passo 1
Fala pessoal!! Bora fazer essa questão comigo??
Para resolver essa questão, podemos começar fazendo as seguintes suposições:
(1) Estado estacionário.
(2) Transferência de calor insignificante da caixa para os arredores.
(3) Condução unidimensional na placa de base.
(4) A troca de radiação na superfície da placa de base é com grandes arredores.
(5) Condutividade térmica constante.
Os dados fornecidos foram:
Condutividade térmica do alumínio:
Espessura da placa de alumínio:
Largura da placa de alumínio:
Temperatura do ar ambiente e grandes arredores:
Emissividade da placa:
Coeficiente de convecção:
Área da interface de alumínio para alumínio:
Temperatura máxima da superfície:
Propriedades: A interface alumínio-alumínio, preenchida com ar com rugosidade de e pressão de contato (Tabela 3.1): .
Constante Boltzmann:
Passo 2
(a) Como toda a dissipação de calor transferida é através da placa de base, podemos dizer que:
Em que:
Sendo
Passo 3
Para obter , o seguinte balanço de energia deve ser realizado na superfície da placa,
Como
Substituindo todos os dados fornecidos na relação obtida acima, temos:
Resolvendo por meio de uma HP ou outro método de sua preferência, vamos encontrar que:
Passo 4
Com a temperatura obtida no passo anterior, podemos calcular a dissipação de energia
Substituindo os termos da equação pelos dados fornecidos e obtidos, temos:
Passo 5
(b) Com a maior contribuição para a resistência total feita por convecção, um benefício significativo pode ser obtido aumentando o valor de h. A tabela de valores é a seguinte:
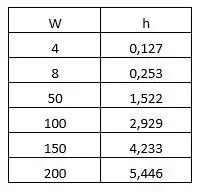
O gráfico fica da seguinte maneira:
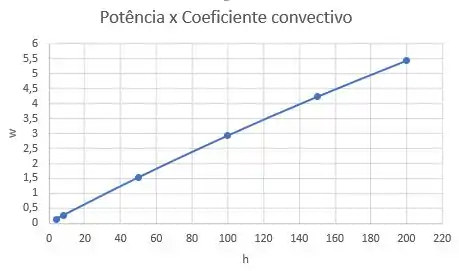
Resposta
(a)
(b) Gráfico no passo 5