Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 85

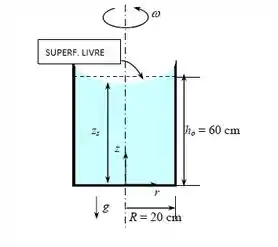
Um contêiner cilíndrico vertical com 40 cm de diâmetro e 90 cm de altura é preenchido parcialmente com água até 60 cm de altura. Agora o cilindro é girado a velocidade angular constante de 120 rpm. Determine quanto cairá o nível do líquido no centro do cilindro como resultado desse movimento de rotação.

Passo 1

Vamos tomar o centro da superfície inferior como a nossa origem, beleza? Isso quer dizer que ali temos r = 0 e z = 0.

Para esse tipo de escoamento, a gente tem que lembrar da bendita equação que é:

z s r = h 0 - w 2 4 g R 2 - 2 r 2

Onde W é nossa velocidade angular que deve ter unidades de rad/s

Vamos substituir nossas variáveis nesse parananuê aí!!

w = 2 π n ˙ = 2 π 120 r e v m i n 1   m i n 60 s = 12,6   r a d / s

A altura verticial do líquido no centro do container aí deve ser calculada, ou seja, no centro, temos r= 0, beleza?

z s 0 = h 0 - w 2 R 2 4 g = 0,6 - 12,6   x   0,2 4 x 9,81 = 0,44   m

Passo 2

Agora, a variação da altura de água no centro vai ser a diferença entre a altura total de água menos a quantidade que abaixou por causa da rotação, certo?

∆ n í v e l = h 0 - Z s 0 = 0,6 - 0,44 = 0,16   m

Resposta

∆ N í v e l = 0,16   m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um muro de arrimo contra um deslizamento de lama deve ser construído colocando-se blocos de concreto retangulares de 0,8 m de altura e 0,2 m de largura ( ρ = 2700k g / m 3 ) lado a lado, como mostra a
Repita o Problema 3-61 para blocos de concreto com 0,4 m de largura.
Repita o Problema 3-63 para um raio de 4 m para a comporta.
Uma comporta na forma de um quarto de círculo e 4 m de comprimento, com raio de 3 m e peso desprezível está ligada com dobradiças à sua aresta superior A , como mostra a Figura P3-63. A comporta contr
Considere uma superfície curva submersa. Explique como você determinaria a componente vertical da força hidrostática que age sobre essa superfície.