Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 63

Uma comporta na forma de um quarto de círculo e 4 m de comprimento, com raio de 3 m e peso desprezível está ligada com dobradiças à sua aresta superior A , como mostra a Figura P3-63. A comporta controla o escoamento da água acima da borda em B , onde é pressionada por uma mola. Determine a força mínima da mola necessária para manter a comporta fechada quando o nível sobe até A na aresta superior da comporta.

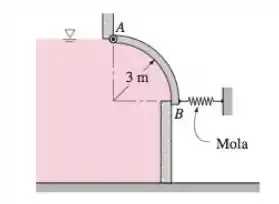
Passo 1

Vamos começar pelas as hipóteses do problema em questão:

  1. A dobradiça não tem atrito;
  2. A pressão atmosférica age em ambos os lados da comporta e por isso pode ser ignorado nos cálculos;
  3. O peso da comporta é desprezível.

Assim o diagrama de corpo livre da comporta pode ser observado abaixo

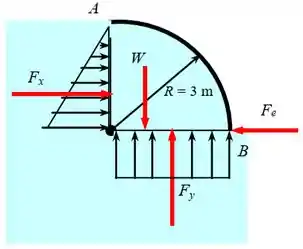
Passo 2

A força hidrostática resultante F R pode ser determinada a partir dos componentes horizontal e vertical F H e F V . A componente horizontal é:

F H = F x = P m é d A = ρ g h C A = ρ g R 2 A

F H = 1000 ⋅ 9,81 ⋅ 3 2 ⋅ 4 ⋅ 3 = 176   k N

Para determinar a componente vertical, vamos obter F y e W . Temos:

F y = ρ g h C A = ρ g h i n f e r i o r A = 1000 ⋅ 9,81 ⋅ 3 ⋅ 4 ⋅ 3 = 353,2   k N

W = ρ g V = ρ g w ⋅ π R 2 4 = 1000 ⋅ 9,81 ⋅ 4 ⋅ π ⋅ 3 4 = 277,4   k N

Assim, a componente vertical é:

F V = F y - W = 353,2 - 277,4 = 75,8   k N

A intensidade e a direção da força hidrostática resultante são:

F R = F H 2 + F V 2 = 176,6 2 + 75,8 2 = 192,2   k N

tan ⁡ θ = F V F H = 75,8 176,6 = 0,429 → θ = 23,2 °

Passo 3

A configuração da ação da força resultante pode ser vista abaixo:

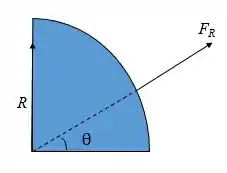
Para obtermos a mínima força requerida na mola, fazemos o somatório de momentos em A entre a força resultante e a força da mola:

∑ M A = 0 → F R R sin ⁡ 90 ° - θ - F e R = 0

F e = F R sin ⁡ ( 90 - θ ) = 192,2 sin ⁡ ( 90 ° - 23,2 ° ) = 177   k N

Resposta

F e = 177   k N

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A válvula de retenção abaixo cobre uma abertura com diâmetro de 22,86 cm em uma parede inclinada. A articulação está a 15 cm da linha de centro, como mostrado. A válvula abrirá quando o momento na art
A comporta ABC na Figura P2.98 tem um quarto de círculo com 2,4 m de largura normal ao papel. Calcule as forças hidrostáticas horizontal e vertical sobre a comporta e a linha de ação da força resultan
O painel curvo BC da Figura P2.96 é um arco de 60°, perpendicular ao fundo em C. Se o painel tiver 4 m de largura, calcule a força hidrostática resultante da água sobre o painel.
Uma esfera de 0,6 m de diâmetro, pesando 1.780 N, fecha um furo de 0,3 m de diâmetro no fundo do tanque da Figura P2.99. Calcule a força F necessária para desalojar a esfera do furo.
A comporta AB da figura abaixo tem três oitavos de círculo, com 3 m de largura, é articulada em B e está apoiada contra uma parede lisa em A. Calcule as forças de reação nos pontos A e B.