Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 3.Problemas - Ex. 61
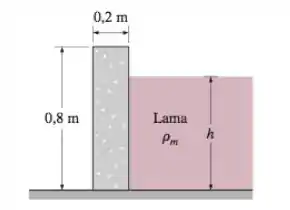
Um muro de arrimo contra um deslizamento de lama deve ser construído colocando-se blocos de concreto retangulares de 0,8 m de altura e 0,2 m de largura () lado a lado, como mostra a Figura P3-61. O coeficiente de atrito entre o solo e os blocos de concreto é = 0,3, e a densidade da lama é de cerca de 1800 kg/m³. Existe a preocupação de que os blocos de concreto deslizem ou escapem da aresta esquerda inferior à medida que o nível de lama suba. Determine a altura da lama na qual (a) os blocos superarão o atrito e começarão a deslizar e (b) escaparão.
Passo 1
Vamos começar com as hipóteses:
- A pressão atmosférica age em ambos os lados da parede e assim pode ser ignorada nos cálculos;
- A linha de ação da força hidrostática passa pelo centro de pressão.
Para determinarmos a altura em cada caso, precisamos obter a força hidrostática resultante. Para isso, primeiro fazemos um diagrama de corpo livre do muro:
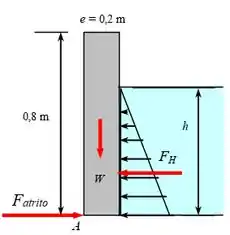
Passo 2
Para determinarmos a força de atrito nos blocos, vamos obter o peso dos blocos:
A força hidrostática que age sobre o muro é:
Igualando a força de atrito com a força hidrostática, a altura para que os blocos superem o atrito será:
Passo 3
Para obtermos a altura em que os blocos escaparão, fazemos o somatório de momentos em A:
Observe que a linha de ação da força hidrostática passa pelo centro de pressão, que nesse caso coincide com o centroide do triângulo formado pela ação da pressão, igual a 2h/3 a partir da superfície livre. A linha de ação do peso do muro passa no plano médio do mesmo. Logo: