Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 27
O controlador de temperatura de um secador de roupas é constituído por uma chave bimetálica montada em contato com um aquecedor elétrico, que se encontra preso a uma junta isolante que, por sua vez, se encontra montada sobre a parede do secador.
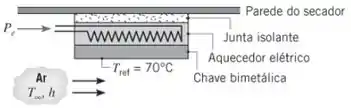
A chave é especificada para abrir a , que é a temperatura máxima do ar de secagem. A fim de operar o secador a uma temperatura do ar mais baixa, uma potência suficiente é fornecida ao aquecedor de tal modo que a chave atinge quando a temperatura do ar é inferior a . Sendo o coeficiente de transferência de calor por convecção entre o ar e a superfície exposta da chave, com , igual a qual é a potência do aquecedor necessária quando a temperatura desejada para o ar no secador é de?
Passo 1
Bora mais uma questão de convecção! Aqui nós temos um secador com um ponto de ajuste a uma temperatura de referência através de uma chave bimetálica. Além do coeficiente de transferência de calor por convecção entre o ar do secador de roupas e a superfície exposta do interruptor.
Então os dados em relação a chave bimetálica são,
E os dados do ar,
Com esses dados, queremos descobrir qual é a potência necessário do aquecedor, , quando . Eu sei que é muita informação, mas com calma a gente consegue resolver esse problema, ta bem? Então vamos lá!
Passo 2
Vamos assumir que:
- Estamos em condição de estado estacionário;
- O aquecedor elétrico é perfeitamente isolado da parede do secador;
- O aquecedor e a chave estão a uma temperatura uniforme (isotérmica) em ;
- A transferência de calor é desprezível dos lados do aquecedor ou da chave;
- A superfície do interruptor, , perde calor apenas por convecção.
Show! Agora vamos olhar apenas para a chave bimetálica e definir um volume de controle nela em que ocorre a entrada de calor do aquecedor e a transferência de calor por convecção para o ar do secador. Equacionando isso temos:
Então, a potência requerida é:
Agora podemos substituir os valores.
Passo 3
Substituindo as informações que vimos no Passo 1, ficamos com:
Esse tipo de controlador é barato e muito eficaz pois pode atingir temperaturas variáveis do ar em operação com um único interruptor de ponto de ajuste.