Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 30
Uma sonda interplanetária esférica, de diâmetro , contém eletrônicos que dissipam . Se a superfície da sonda possui uma emissividade de e não recebe radiação de outras fontes como, por exemplo, do Sol, qual é a sua temperatura superficial?
Passo 1
Vamos para mais uma questão então? \o/. Aqui nós temos o diâmetro e emissividade da sonda interplanetária esférica e dissipação de energia na sonda, sendo esta sonda inserida em um meio que não emite radiação. Então vai ficar assim:
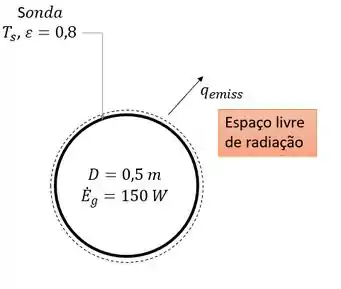
E temos que calcular a temperatura da superfície da sonda. Então vamos para as nossas considerações.
Passo 2
Assumindo que estamos em uma condição de estado estacionário e que a radiação na sonda é desprezível, como o próprio enunciado disse, vemos que a conservação de energia determina um equilíbrio entre a geração de energia dentro da sonda e a emissão de radiação da superfície da sonda. Então, a qualquer instante:
Sabendo que,
Como queremos a temperatura superficial da sonda, vamos isolar o da equação,
Como a sonda é esférica, vamos ter que a área superficial, vai ser:
Substituindo na nossa expressão da temperatura superficial:
Lembrando que esse é a Constante de Stefan-Boltzmann, beleza?
Passo 3
Agora que já manipulamos a equação (ufa!), podemos substituir os valores fornecidos pelo enunciado.
Repara que, se fossemos considerar a radiação do sol essa temperatura seria bem maior.