Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 23
Uma caixa de transmissão, medindo de lado, recebe uma entrada de potência de vinda do motor.
Sendo a eficiência de transmissão ; com o escoamento do ar caracterizado por e qual é a temperatura superficial da caixa de transmissão?
Passo 1
O desenho do enunciado possui alguns detalhes que não vão fazer diferença na resolução, então simplifiquei a caixa de transmissão para um cubo, show? Vamos lá então... Nós temos a largura, potência de entrada e eficiência da caixa de transmissão. Além disso, temos o coeficiente de temperatura e convecção associado ao fluxo de ar sobre o revestimento. Então ficamos com o esquema abaixo:
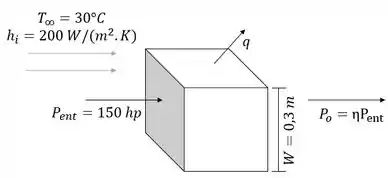
Dado isso, queremos encontrar a temperatura superficial da caixa de transmissão.
Passo 2
Para resolver essa questão vamos assumir que:
- Estamos em condição de estado estacionário;
- O coeficiente de convecção e a temperatura superficial são uniformes em toda a caixa;
- A radiação é desprezível.
Com isso em mente, podemos utilizar a Lei de Newton de resfriamento:
Onde a área superficial da caixa de transmissão, é definida por:
Então,
O nosso objetivo é encontrar , certo? Então vamos isolar da equação acima ficando com:
Mas primeiro, precisamos ver quem é esse .
Passo 3
A taxa de calor nada mais é que energia, e a potência de saída da caixa de transmissão é , então a taxa de calor pode ser representada por:
Substituindo os valores ficamos com:
Lembrando que nós, SEMPRE, precisamos colocar os nossos dados em SI. Então nesse caso tivemos que transformar em , beleza?
Substituindo agora na equação para finalmente encontrar a temperatura superficial,
Esse valor, na realidade, representa um valor médio da temperatura de superfície, considerando a variação do coeficiente de convecção.