Deduza expressões para o fator de forma F12 associado aos arranjos a seguir. Expresse os seus resultados em termos de A1, A2 e qualquer outra área de superfície hipotética apropriada, assim como do fator de forma para discos paralelos coaxiais (Tabela 13.2, Figura 13.5).

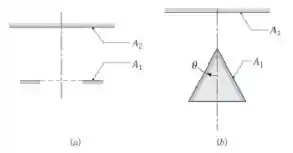
1. Um disco circular e um anel coaxial.
2. Um disco circular e um cone circular coaxial. Esboce a variação de F12 com θ para 0 ≤ θ ≤ π/2 e explique as características marcantes

Agora nós precisamos esboçar a variação de … Vamos nessa!

Para isso, vamos começar definindo uma superfície , de modo que:

E por reciprocidade vamos ter:

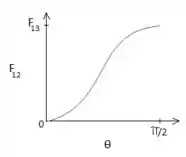
Teremos então que a variação do nosso em função de , terá esse comportamento:

Ou seja, no limite quando , o cone se aproxima de um disco de área . E quando a área do cone diminui e temos que:

Esboçando em um gráfico, temos o seguinte:

Prontinho! Arrasamos!