58 – Um pistão sem atrito de diâmetro Dp = 50 mm, espessura δ = 10 mm, e densidade ρ = 8000 kg/m3 é colocado em um cilindro vertical de comprimento total L = 100 mm. O cilindro é perfurado em um material de baixa condutividade térmica, e uma massa de ar Mar = 75x10-6 kg é anexado no volume abaixo do cilindro. A vizinhança está a Tviz = 300 K enquanto que a superfície do fundo do cilindro é mantida a T1. A emissividade de todas as superfícies é ε = 0,3.

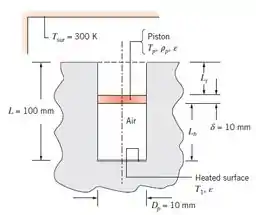
Qual é a distância entre o fundo do pistão e o fundo do cilindro, Lb, para T1 = 300, 450 e 600 K? Qual é a temperatura do pistão? Dica: Negligencie a taxa de transferência de calor por convecção e assume que a temperatura média do ar é Tar = (Tp + T1)/2.

Considerando o ar como um gás ideal, podemos usar a equação de Clapeyron, que é eq. dos gases ideais:

Onde,

-Par é a pressão do ar no cilindro;

-Var é o volume do ar dentro do cilindro;

-nar é o nº de mols do ar;

-R é a constante dos gases ideais, R = 8,314 kJ/kmol.K;

-Tar é a temperatura do ar.

Lembrando que o nº de mols pode ser relacionado com a massa da seguinte forma

Onde, MMar é a massa molar do ar

Assim,

Pela informação do enunciado

Onde, Tp é a temperatura do pistão

Para encontrarmos a pressão do ar, Par, podemos fazer um balanço de forças sobre o ar, que neste caso a pressão absoluta do ar pode ser determinada pela soma entre a força peso que o pistão exerce sobre o ar com a pressão atmosférica exercida sobre o pistão, assim

Onde,

-Ap e Fp são, respectivamente, a área de seção transversal do pistão e a força peso do pistão.

Onde, mp é a massa do pistão e g a constante de gravidade

Assim,

Substituindo essas relações no balanço de força:

Para o volume do ar, Var, que é o volume do ar dentro do cilindro, compreendido entre o fundo do cilindro e o fundo pistão, assim o volume será dado pela seguinte expressão

Sendo que Lb é justamente a distância entre o fundo cilindro e o fundo do pistão que precisamos encontrar. Assim, isolando Lb

Sendo que pela eq. dos gases ideais o Var é:

Assim,

Vamos precisar determinar a temperatura do pistão, Tp, para encontrarmos a temperatura do ar. Para isso, podemos encontrar fazendo um balanço de energia.

Vamos agora fazer um balanço de energia. Um balanço de energia que pode ser feito é uma transferência de calor associada ao invólucro formado entre o fundo do cilindro e o fundo do pistão, que será, pela eq. 13.30 do Incropera:

Analogamente, para um balanço de energia no topo do pistão e a vizinhança:

Um balanço de energia global, vai resultar em

Onde,

Os parâmetros Ebi’s são as potências de emissão associadas a cada superfície, considerando superfícies negras, assim

Onde, σ é a constante de Stefan-Boltzmann

Assim,

Vamos tentar isolar Tp:

Onde,

Isolando Tp

O parâmetro k depende dos parâmetros F são os fatores de forma.

As eq’s para os fatores de forma são encontrados na Tabela 13.2, considerando discos paralelos coaxiais. Assim, as eq’s para os fatores de forma são:

Onde,

Assim, como temos que os fatores de forma dependem de Lb, e Lb dependem de de Tp, assim teremos que realizar um método iterativo para calcular a temperatura do pistão.

O algoritmo (passo a passo) que você pode seguir para solucionar este problema por um método iterativo é o seguinte:

• Chute inicial para Tp (Tp0)
• Calcula Tar
• Calcula Lb
• Calcula Lt
• Calcula os fatores de forma
• Calcula o parâmetro k
• Calcula Tp
• Calcular erro percentual
• Se o erro for muito pequeno, finalizar iteração, caso contrário, fazer Tp0 = Tp e recomeçar iteração. Realizar iterações até que o erro seja muito pequeno, por volta de 10-5, por exemplo.

Resolvendo pelo EXCEL:

-Para T1 = 300 K:

-Para T1 = 450 K:

-Para T1 = 600 K: