Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 13.Problemas - Ex. 02

Considere as seguintes fendas, cada uma com largura W, que foram usinadas em um bloco de material sólido.

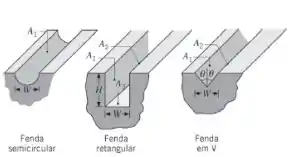
  1. Para cada caso, obtenha uma expressão para o fator de forma da fenda com relação à vizinhança fora da fenda.
  2. Para a fenda em forma de V, obtenha uma expressão para o fator de forma F12, sendo A1 e A2 as superfícies opostas.
  3. Se H = 2 W na fenda retangular, qual é o fator de forma F12?

Passo 1

Fala aí! Vamos resolver essa questão juntos, beleza? Partiu!!

Bom, nosso enunciado pediu quer que a gente resolva essas três letrinhas… Vamos nessa!

Primeiro a letra a, vamos conseguir a expressão para o fator de forma de cada figura… Começando pela fenda semicircular:

F 21 = 1,0

E por reciprocidade:

F 12 = A 2 A 1   .   F 21

F 12 = W π   .   W / 2   .   1

F 12 = 2 π

Agora para a fenda retangular:

F 4   1,2 , 3 = 1

Por reciprocidade, temos:

F 1,2 , 3   4 = A 4 A 1 + A 2 + A 3   .   F 4   1,2 , 3

F 1,2 , 3   4 = W H + W + H   .   1

F 1,2 , 3   4 = W W + 2   .   H

E por último para a fenda em V:

F 3   1,2 = 1  

Usando a reciprocidade:

F 1,2   3 = A 3 A 1 + A 2   .   F 3   1,2

F 1,2   3 = W W / 2 s e n   θ + W / 2 s e n   θ   .   1

F 1,2   3 = s e n   θ

Partiu letra b!

Passo 2

Agora nós precisamos encontrar a expressão para o fator de forma F 12 na fenda em V… Vamos nessa!

Para isso, vamos usar as equações 13.3 e 13.4, teremos então:

F 12 = 1 - F 13

F 12 = 1 - A 3 A 1   .   F 31

E sabendo que por simetria, vamos ter que:

F 31 = 1 2

Vamos ter:

F 12 = 1 - W W / 2 / s e n θ   .   1 2

F 12 = 1 - s e n   θ

Show! Vamos para a letra c!

Passo 3

Pra fechar, letra c! Ela pediu pra gente a forma F 12 da fenda retangular… Bom, pra isso vamos precisar visitar a figura 12.4 e tirar de lá a relação:

X L = H W = 2 e Y L → ∞

Sendo assim, nosso F 12 será aproximadamente:

F 12 ≈ 0,62

Uhul! Arrasamos!

Resposta

  1. Passo 1.

  2. F 12 = 1 - s e n   θ

  3. F 12 ≈ 0,62
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

35 – Duas grandes placas paralelas são mantidas a T1 = 500 K e T2 = 300 K, respectivamente. A placa quente tem uma emissividade de 0,9 enquanto que a placa fria tem emissividade de 0,7.A) Determine o
32 – A eq. 1.7 é subjetiva a diversas restrições, tal como a vizinhança sendo isotérmica e grande em relação a superfície menores. Considere uma superfície pequena e grande de esferas concêntricas de
48 – Um longo condute é construído com paredes amplas cinzas e difusivas de 0,5 m. O topo e o fundo do condute está isolado. As emissividades das paredes são ε1 = 0,45, ε2 = 0,65 e ε3 = 0,15, respecti
2 – Uma partícula esférica de raio r1= 5 mm está suspensa por um fio fino dentro de um tubo cilíndrico de raio interno r2 = 15 mm e comprimento L = 0,5 m. Determine os fatores de forma F11, F12, F13 e
64 – Três grandes barras cilíndricas de diâmetro D = 20 mm estão para ser termicamente tratadas em um forno. As barras estão inicialmente a uma temperatura de 300 K, enquanto que as paredes do forno e