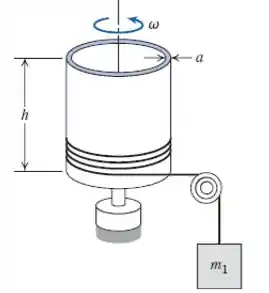
O delgado cilindro externo (massa m2 e raio R) de um pequeno viscosímetro portátil de cilindros concêntricos é acionado pela queda de uma massa, m1, ligada a uma corda. O cilindro interno é estacionário. A folga entre os cilindros é a. Desprezando o atrito do mancal externo, a resistência do ar e a massa do líquido no viscosímetro, obtenha uma expressão algébrica para o torque devido ao cisalhamento viscoso que atua no cilindro à velocidade angular ω. Deduza e resolva uma equação diferencial para a velocidade angular do cilindro externo como função do tempo. Obtenha uma expressão para a velocidade angular máxima do cilindro.

Fala aí galera, vamos para mais um problema de mecânica dos fluidos

Sabemos que:

Para um fluido newtoniano com perfil de velocidade linear:

Também sabemos que o torque é dado por:

Para equilíbrio:

Logo, isolando na segunda equação e substituindo na primeira:

Essa é a Edo pedida, mas como o foco aqui não é a resolução delas, vamos pular esta parte. Resolvendo a EDO: