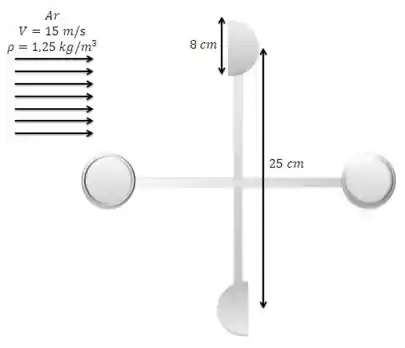
Uma turbina eólica com duas ou quatro conchas hemisféricas conectadas a um pivô é usada comumente para medir a velocidade do vento. Considere uma turbina de vento com duas conchas de de diâmetro com uma distância de centro a centro de , conforme mostra a Figura . O pivô está preso devido a um defeito mecânico e as conchas não estão girando. Para um vento com velocidade de e densidade do ar de , determine o torque máximo que a turbina aplica ao pivô.
Passo 1
Olá, tudo bem? Vem comigo resolver essa atividade?!
Este é um problema de Dinâmica de Fluidos (Arrasto) que trata do torque máximo exercido por um anemômetro de conchas (turbina eólica) que está fixo. O torque é gerado pela diferença nas forças de arrasto entre as conchas que enfrentam o vento e as conchas que se afastam dele.
Os dados que a gente tem são:

O torque máximo ocorre quando uma concha está totalmente exposta ao vento (máximo arrasto) e a concha oposta está oferecendo o arrasto mínimo (devido ao seu formato).
Passo 2
A força de arrasto sobre um corpo é dada por:
Onde é o coeficiente de arrasto e é a área de projeção frontal (para uma hemisfera de diâmetro ,
O diagrama mostra quatro conchas, mas a simetria sugere que apenas as duas conchas verticais (perpendiculares ao fluxo) contribuem para o torque. A concha que está de frente para o vento (aberta) gera um grande torque, enquanto a concha que está de costas (convexa) gera um pequeno torque oposto.
Para o torque máximo, assumimos que as duas conchas horizontais (lado esquerdo e direito, onde ) não contribuem para o torque (o problema está em regime estático).
Máximo Arrasto - Abertura voltada para o vento
Mínimo Arrasto - Lado convexo voltado para o vento
Passo 3
O torque é , onde é o braço da alavanca:
O torque máximo é a diferença entre o torque positivo (gerado pela Concha ) e o torque negativo (gerado pela Concha ):