Desenvolva expressões análogas às (11.16) e (11.17), utilizando, respectivamente, a pressão parcial e a concentração do soluto.

Para resolver essas questões que envolvem teoria do duplo filme precisamos desenhar o duplo filme, fica mais claro, então meu desenho vai ficar algo mais ou menos assim:

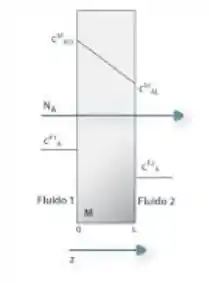
Para primeira demonstração vamos utilizar a teoria das pressões parciais, então o fluxo na fase gasosa deve ser algo do tipo:

E o fluxo na fase líquida devemos ter algo, mais ou menos, assim:

Onde temos que e , são os coeficientes globais de transferência que relaciona todas as resistências relacionadas a transferência de massa do sistema e , é as pressões parciais e a concentração do componente no seio da fase fluida.

Só que medir esses coeficientes globais é horrível, sendo assim vamos procurar uma maneira mais simples de medi-los que é exprimindo-os em função dos coeficientes locais de transferência.

Para isso, primeiramente, vamos admitir que o soluto está pouco difundido dentro do fluido 2, porque assim podemos utilizar o estado padrão de henry da termodinâmica que diz que existe um equilíbrio linear da seguinte forma:

E temos que a concentração do componente A na fase líquida também deve estar em equilíbrio com a concentração da fase gasosa:

Impondo a condição do estado estacionário, temos que os fluxos de matéria são iguais, portanto, temos que os fluxos e matéria na interface do filme é dado por:

Onde e são os coeficientes locais de transferência de massa e e é as pressões parciais e a concentração do componente no filme.

Portanto temos que:

Utilizando a equação de fluxo total, temos que:

Somando e subtraindo temos que:

Utilizando as relações de equilíbrio temos que:

Utilizando as seguintes expressões de fluxo:

temos que:

Realizando os mesmos passos para a segunda equação temos:

Somando e subtraindo temos que:

Utilizando as relações de equilíbrio temos que:

Utilizando as expressões de fluxo locais temos que: