Um detector de microescala monitora um escoamento em regime estacionário , de ar em relação à possível presença de matéria particulada pequena e perigosa, que pode estar suspensa no ambiente. O sensor é aquecido até uma temperatura um pouco superior com objetivo de induzir uma reação química associada a certas substâncias de interesse, que podem colidir na superfície ativa do sensor. A superfície ativa produz uma corrente elétrica se tais reações ocorrerem na superfície e a corrente elétrica é, então, enviada para um alarme. Para maximizar a área da superfície da cabeça do sensor e, desta maneira, a probabilidade de captura e detecção de uma partícula, a cabeça do sensor é projetada com uma forma muito complexa. O valor do coeficiente de transferência de calor médio associado ao sensor aquecido deve ser conhecido de modo que a potência elétrica requerida pelo sensor possa ser determinada.

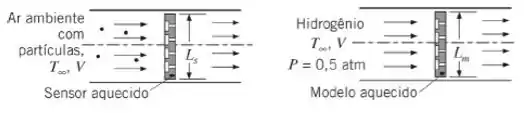
Seja um sensor com uma dimensão característica de . Um modelo em escala do sensor encontra-se posicionado em um túnel de vento com recirculação (fechado) usando hidrogênio como fluido de trabalho. Se o túnel de vento opera com uma pressão absoluta de hidrogênio de e uma velocidade , ache a temperatura do hidrogênio e a dimensão característica do modelo em escala, , requeridas.

Sabemos que embora o número de Prandtl seja independente da pressão para um gás ideal, a viscosidade cinemática depende da pressão.

Assim, temos que a viscosidade cinemática de hidrogénio muda com a pressão absoluta em :

Para um gás ideal:

Como:

Pela similaridade:

Dados:

.

Temos: