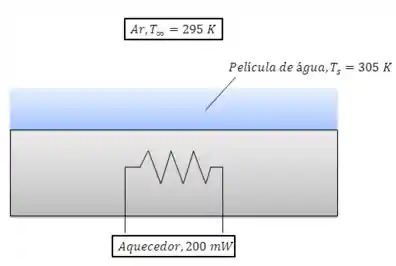
Um disco com de diâmetro está coberto por uma película de água. Sob condições de regime estacionário, um aquecedor com potência de é necessário para manter o sistema disco-película de água a em meio ao ar seco a . A taxa de evaporação observada é igual a .

(a) Calcule o coeficiente de transferência de massa por convecção médio, , para o processo de evaporação.

(b) Calcule o coeficiente de transferência de calor por convecção médio, .

(c) Os valores de e satisfazem a analogia termo-mássica?

(d) Sendo a umidade relativa do ar ambiente, a , aumentada de (ar seco) para , mas o suprimento de energia para o aquecedor mantido em , a taxa de evaporação aumenta ou diminui? A temperatura no disco aumenta ou diminui?

Vamos agora para o item (b). Neste item devemos obter o coeficiente de transferência de calor por convecção.

Como primeiro passo, vamos fazer um balanço de energia no sistema. Considerando que estamos em regime estacionário e que não há geração de energia ficamos com:

Para este sistema temos energia sendo fornecida pelo aquecedor e perdas de calor por convecção e evaporação. Então:

Podemos escrever as taxas de transferência como:

E

Em que

De acordo com os dados da tabela A-6 do apêndice A para água a .

Substituindo na relação de balanço de energia:

Agora que temos os coeficientes de transferência de massa e calor podemos ir para o item (c). Neste item devemos verificar se estes coeficientes atendem à analogia termo-mássica.

A analogia é dada por:

Vamos calcular separadamente cada lado da equação e verificar se encontramos valores similares. Tudo bem?

Começando com o lado esquerdo:

Para o lado direito precisaremos das propriedades do ar na temperatura de filme. A temperatura de filme é:

Pelas tabelas A-4 e A-8 do apêndice A:

Vamos agora calcular o número de Lewis:

O lado direito da equação é:

Como chegamos em valores distintos concluímos que a analogia não é válida para este caso

Passamos agora ao item (d). Vamos avaliar o que aconteceria se aumentarmos a umidade relativa do ar para .

Primeiro, com relação à taxa de evaporação. Ela é dada por:

Para o caso anterior consideramos , mas agora, . Então, a diferença irá ter um valor menor. Considerando que o coeficiente de transferência de massa e a área se mantém, podemos esperar que a taxa de evaporação irá diminuir. Tudo bem?

Veremos agora o que ocorre com a temperatura do disco. Pelo balanço de energia vimos que:

Aplicando as relações para taxa de calor perdida por evaporação e convecção:

Como acabamos de ver, a taxa de evaporação diminuiu então, a diferença terá um valor superior ao que encontramos anteriormente. Considerando que o coeficiente convectivo, a área do disco e a temperatura do ar irão se manter constantes, a única forma de manter a igualdade é se a temperatura do disco aumentar.