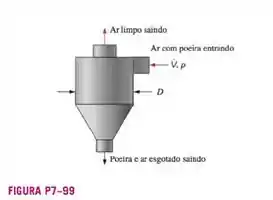
Um dispositivo comum usado em diversas aplicações para limpar o ar carregado de partículas é o ciclone de escoamento reverso (Figura). O ar com poeira (vazão em volume e densidade ) entra tangencialmente através de uma abertura na lateral do ciclone e gira ao redor do tanque. As partículas de poeira são lançadas para fora e caem na parte inferior, enquanto o ar limpo é tirado para a parte superior. Os ciclones de escoamento reverso em estudo são todos geometricamente semelhantes. Assim, o diâmetro D representa a única escala de comprimento necessária para especificar completamente toda a geometria do ciclone. Os engenheiros estão preocupados com a queda de pressão através do ciclone.

(a) Gere uma relação adimensional entre a queda de pressão através do ciclone e os

parâmetros dados. Mostre todo o seu trabalho;

(b) Se o tamanho do ciclone dobrar, com todas as outras condições iguais, por qual fator a queda de pressão variará?

(c) Se a vazão em volume dobrar, com todas as outras condições iguais, com qual fator a

queda de pressão variará?

Vamos lá! Isso nada mais é do que uma questão que envolve análise dimensional e semelhança!!!

Vamos começar a nossa letra a então!!

(a) Gere uma relação adimensional entre a queda de pressão através do ciclone e os

parâmetros dados.

Pra começar, vamos listar as variáveis relavantes:

Daqui a gente já consegue ver o número de parâmetros, que são , então:

Agora a gente precisa listar as dimensões primárias de cada parâmetro!

Vamos começar por :

Agora a densidade, :

Vazão volumétrica, :

Diâmetro, D:

Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões e , então podemos considerar:

Teorema de Pi de Buckingham:

O a gente já tinha achado no Passo 1, lá vimos que !

Substituindo:

Nesse caso o número de grupos esperado é igual a . Então vamos atrás dele!!

Para isso, precisamos decidir quais vão ser os parâmetros repetidos.

Temos e , como é o parâmetro dependente a nossa única opção é escolher e como parâmetros repetidos.

Agora sim, vamos encontrar o nosso grupo !!

Organizando os nossos parâmetros a gente fica com:

Eles tem que ter dimensão zero, como a gente ta vendo no lado esquerdo da igualdade! Agora vamos substituir esses parâmetros pelas suas respectivas dimensões primárias!

Agora vamos equacionar os expoentes de uma dimensão de cada vez, começando pela massa:

Massa:

Tempo:

Comprimento:

Então ficamos com:

Agora que a gente conhece os expoentes, vamos substituir:

Organizando:

Como só temos um grupo ele não pode ser função de outros grupos , logo dizemos que ele é igual a uma contante:

Com isso a relação que o enunciado pediu, fica: