Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 101

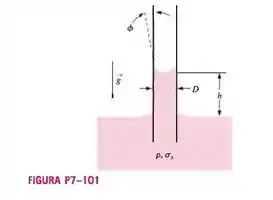
Quando um tubo capilar de diâmetro pequeno D é inserido em um contêiner de líquido, o líquido se eleva até a altura h dentro do tubo (Figura). h é uma função da densidade do líquido

p, do diâmetro do tubo D, da constante gravitacional g, do ângulo de contato ϕ   e da tensão superficial σ s do líquido

  1. Gere uma relação adimensional para h como função dos parâmetros dados.

  2. Compare seu resultado com a equação analítica exata para h dada no Capítulo 2. Os resultados de sua análise dimensional são consistentes com a equação exata? Discuta.

Passo 1

Bora então começar vendo essa letra (a)?!

Para resolver esse exercício, vamos pegar todas as informações do enunciado, fazer o passo a passo do método das variáveis repetidas !

Então vamos começar reunindo os parâmetros dimensionais que descrevem o problema!

h = f ( ρ , g , σ s , D , ϕ )

Daqui a gente já consegue ver o número de parâmetros:

n = 6

Passo 2

Agora a gente precisa listar as dimensões primárias de cada parâmetro!

Então vamos começar pelo h :

{ h } = { L }

A densidade, ρ :

ρ = { m 1 L - 3 }

Agora a gravidade, g :

g = { L 1 t - 2 }

E por fim a tensão superficial, σ s :

{ σ s } = m 1 t - 2

Diâmetro do tubo:

D = { L }

Ângulo de contato, ϕ :

ϕ = { 1 }

Isso porque aqui o ângulo de contato não tem dimensão!!

Passo 3

Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões m ,   L e t , então podemos considerar:

j = 3

Teorema de Pi de Buckingham:

k = n - j

O n a gente já tinha achado no Passo 1, lá vimos que n = 6 !

Substituindo:

k = 6 - 3 = 3

Nesse caso o número de grupos π esperado é igual a 3 . Então vamos atrás deles!!

Passo 4

Antes de começar a precisamos decidir quais vão ser os 3   parâmetros repetidos.

h é o parâmetro dependente, não podemos escolher ele, ϕ é adimensional, também não serve, restam as opções ρ , g , σ s   e   D !

Eu vou escolher ρ , g , D por serem os parâmetros mais simples!

Passo 5

Agora sim, vamos encontrar o nosso primeiro grupo π !!

Começando com o π 1 que vai ser o π dependente!!

Organizando os nossos parâmetros a gente fica com:

π 1 = 1 = { ( h ) × ρ a × g b D c }

Eles tem que ter dimensão zero, como a gente ta vendo no lado esquerdo da igualdade! Agora vamos substituir esses parâmetros pelas suas respectivas dimensões primárias, que a gente listou lá no Passo2:

π 1 = m 0 L 0 t 0 = { ( L 1 ) × m 1 L - 3   a × L t - 2 b L c }

Agora vamos equacionar os expoentes de uma dimensão de cada vez, começando pela massa:

Massa:

m 0 = ( m 1 a }

0 = a  

Comprimento:

L 0 = { L 1 L - 3 a L 1 b L 1 c }

0 = 1 - 3 a + b + c

0 = 1 + b + c

Tempo:

t 0 = ( t - 2 b }

0 = - 2 b

Logo:

0 = 1 + 0 + c

c = - 1

Agora que a gente conhece os expoentes, vamos substituir:

π 1 = 1 = { ( h ) × ρ 0 × g 0 D - 1 }

Organizando:

π 1 = h D

Agora vamos achar π 2 , esse vai ser nosso primeiro π independente combinando as nossas variáveis repetidas com σ s :

π 1 = 1 = { ( σ s ) × ρ a 2 × g b 2 D c 2 }

π 1 = m 0 L 0 t 0 = { ( m 1 t - 2 ) × m 1 L - 3   a 2 × L t - 2 b 2 L c 2 }

Agora vamos equacionar os expoentes de uma dimensão de cada vez, começando pela massa:

Massa:

m 0 = m 1 ( m 1 a 2 }

0 = 1 + a 2  

a 2 = - 1

Comprimento:

L 0 = { L - 3 a 2 L 1 b 2 L 1 c 2 }

0 = - 3 a 2 + b 2 + c 2

0 = 3 + b 2 + c 2

N × s m = k g × m s 2 × s m = m t

Tempo:

t 0 = t - 2 ( t - 2 b 2 }

0 = - 2 - 2 b 2

b = - 1

Logo: 0 = 3 + b 2 + c 2

c = - 2

Agora que a gente conhece os expoentes, vamos substituir:

π 1 = 1 = { ( σ s ) × ρ - 1 × g - 1 D - 2 }

Organizando:

π 2 = σ s ρ g D 2

Agora temos que achar π 3 , esse vai ser nossosegundo π independente combinando as nossas variáveis repetidas com ϕ .

Mas lembra que ϕ   não tem dimensão?!!

Então:

π 3 = ϕ

Passo 6

Agora podemos responder a letra (a)!

  1. Gere uma relação adimensional para h como função dos parâmetros dados.

    2. h D = f σ s ρ g D 2 , ϕ

    Passo 7

    Agora vamos ver a letra (b):

  2. Compare seu resultado com a equação analítica exata para h   dada no Capítulo 2. Os resultados de sua análise dimensional são consistentes com a equação exata? Discuta.

A solução analítica é:

h = 4 σ s ρ g D cos ⁡ ϕ

Comparando com a nossa equação:

h D = f σ s ρ g D 2 , ϕ

Elas são muito parecidas, a gente pode escrever uma relação entre as duas assim:

π 1 = c o n s t a n t e × π 2 × cos ⁡ π 3

Ou:

h D = 4 × σ s ρ g D 2 × cos ⁡ ϕ

A gente percebe que existe sim uma consistencia entre as duas soluções, no entanto a gente precisaria de experimentos para chegar na solução analítica!

Uhuuuul, acabamos!!!

Resposta

  1. h D = f σ s ρ g D 2 , ϕ ;

  2. h D = 4 × σ s ρ g D 2 × cos ⁡ ϕ .
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere um líquido em um contêiner cilíndrico no qual tanto o contêiner quanto o líquido giram como um corpo rígido (rotação de corpo sólido). A diferença de elevação h entre o centro da superfície
Repita o problema 7-46, mas com um parâmetro independente adicional incluído: a velocidade do som c no fluido. Use o método de várias variáveis repetidas para gerar uma relação adimensional para a fre
Considere o caso no qual o contêiner e o líquido do Problema 7-44 estão inicialmente em repouso. Em t = 0, o contêiner começa a girar. É preciso algum tempo para que o líquido gire como um corpo rígid
Miguel está trabalhando em um problema que tem uma escala de comprimento característica L , uma velocidade característica V , uma diferença de densidade característica Δ ρ , umadensidade ρ (média) car
Repita o Problema 7-54, exceto que a velocidade do som c de um gás ideal é considerada uma função apenas da pressão P e da densidade do gás ρ . Mostrando todo o seu trabalho, use aanálise dimensional