Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 94

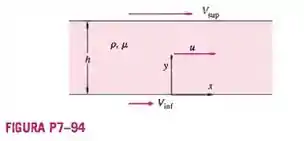
Considere uma variação do problema do escoamento de Couette completamente desenvolvido do Problema 7-52 — o escoamento entre duas placas paralelas finitas separadas pela distância h , com a placa superior se movendo à velocidade V s u p   e a placa inferior se movendo à velocidade V i n f como ilustra a figura. O escoamento é em regime permanente, incompressível e

bidimensional no plano x y . Gere uma relação adimensional para o componente x da velocidade do fluido u como uma função da viscosidade do fluido ρ das velocidades das placas V s u p e V i n f , da distância h, da densidade do fluido ρ e da distância y .

(Sugestão: pense cuidadosamente sobre a lista de parâmetros antes de utilizar a álgebra.)

.

Passo 1

Antes de mais nada vamos prestar atenção na sugestão do enunciado “pense cuidadosamente sobre a lista de parâmetros antes de utilizar a álgebra”

Tendo isso em vista vamos voltar lá na questão 52   e vamos procurar o que mudou de uma questão para a outra!

Depois de ler com muita atenção a gente percebe que na questão 52 apenas a placa superior estava se movendo, enquanto aqui as ambas as placas tem velocidade.

Ahh, no caso da questão 52 a resposta foi:

u V = f ( R e , y h )

Onde R e é o número de Reynolds dado por:

R e = ρ V h μ

Mas peraí, a velocidade é sempre e relação a um ponto, não é?

Por exemplo, na questão 52 tinhamos a velocidade da placa superior, menos a velocidade da placa inferior, mas como a placa inferior estava parada o resultado seria apenas V i n f !

Agora a gente tem velocidade nas duas placas, então temos que calcular a velocidade relativa, e nesse caso é como se uma placa estivesse parada em relação a outra!!

Opa, se é assim a resolução de questão vai ser igual a resolução da questão 52 com a única diferença é que no lugar de V teremos a velocidade relativa, V r :

V r = V s u p e r i o r - V i n f e r i o r

u ( V s u p e r i o r - V i n f e r i o r ) = f ( R e , y h )

E nesse caso R e passa a ser:

R e = ρ ( V s u p e r i o r - V i n f e r i o r ) h μ

Aweee!!!

Resposta

Relação adimensional:

u ( V s u p e r i o r - V i n f e r i o r ) = f ( R e , y h )

Onde R e :

R e = ρ ( V s u p e r i o r - V i n f e r i o r ) h μ

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Quando pequenas partículas de aerossol ou microorganismos se movem através do ar ou da água, o número de Reynolds é muito pequeno ( R e«1 ) « . Tais escoamentos são chamados de escoamentos lentos. O a
Sabe-se que a velocidade do som c em um gás ideal é uma função da razão entre os calores específicos k , da temperatura absoluta T e da constante específica do gás ideal R g á s á (Figura P7-54). Most
Uma pequena partícula de aerossol de densidade ρ p e diâmetro característico D p cai no ar de densidade ρ e viscosidade μ (Figura P7-59). Se a partícula for suficientemente pequena, aaproximação do es
Repita o Problema 7-54, exceto que a velocidade do som c em um gás ideal é considerada uma função da temperatura absoluta T , da constante universal dos gases ideais R u da massamolar (peso molecular)
Repita o Problema 7-54, exceto que a velocidade do som c em um gás ideal é considerada uma função apenas da temperatura absoluta T e da constante específica do gás ideal R g á s á .Mostrando todo o se