Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 99

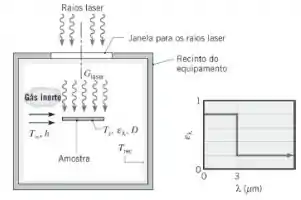
Um dispositivo para o processamento de materiais com laser utiliza uma amostra em forma de um disco, com diâmetro D   =   25   m m e espessura w   =   1   m m . A amostra tem uma superfície difusa, cuja distribuição espectral da emissividade, ε λ ( λ ) , é conhecida. Para reduzir a oxidação, uma corrente de um gás inerte, com temperatura T ∞ =   500   K e coeficiente convectivo h   =   50   W / ( m 2 · K ) , escoa sobre as superfícies superior e inferior da amostra. O recinto do equipamento é grande e tem paredes isotérmicas a T r e c =   300   K . Para manter a amostra a uma temperatura de operação apropriada de T a =   2000   K , um feixe colimado de raios laser com um comprimento de onda de λ   =   0,5   μ m irradia sua superfície superior.

(a) Determine a emissividade total ε da amostra.

(b) Determine a absortividade total α da amostra para a irradiação oriunda das paredes do recipiente.

(c) Efetue um balanço de energia na amostra e determine a irradiação laser, G l a s e r , requerida para manter a amostra a T a =   2000   K .  

(d) Considere um processo de resfriamento após a desativação do laser e do escoamento do gás inerte. Esboce a emissividade total em função da temperatura da amostra, T a ( t ) , durante o processo. Identifique as características principais dessa curva, incluindo a emissividade na condição final do processo ( t   →   ∞ ) .  

(e) Estime o tempo necessário para resfriar a amostra desde sua condição de operação T a ( 0 )   =   2000   K até uma temperatura segura para o toque de T a ( T )   =   40 ° C . Utilize o método da capacitância global e inclua os efeitos da convecção para o gás inerte com h   =   50   W / ( m 2 · K ) e T ∞ = T r e c = 300   K . As propriedades termofísicas do material que compõe a amostra são: ρ = 3900   k g / m 3   ,   c p =   760   J / ( k g   ·   K )   e k   =   45   W / ( m · K ) .

Passo 1

Nessa questão temos aparelhos para processamento de materiais a laser, amostra espectralmente seletiva aquecida à temperatura operacional T s   =   2000   K por irradiação a laser ( 0,5   μ m ) , G l a s e r , experimenta convecção com gás inerte e troca de radiação com o gabinete.

Com isso vamos encontrar a emissividade total da amostra, ε ,   a absorção total da amostra, α , para irradiação do recinto e a irradiação a laser necessária para manter a amostra em T s =   2000   K , fazendo um balanço energético na amostra.

Passo 2

Para resolver essa questão vamos assumir:

(1) O compartimento é isotérmico e grande em comparação com a amostra;

(2) a amostra é opaca e difusa, mas espectralmente seletiva, de modo que ε λ = α λ ;

(3) A amostra é isotérmica.

A emissividade total da amostra, ε , em T s =   2000   K pode ser expresso em termos do fator de emissão da banda,   F ( 0 - λ ,   T )

ε = ε 1 F ( 0 → λ 1 T s ) + ε 2 1 - F 0 → λ 1 T s

ε = 0,8 × 0 , 7378 + 0,2 1 - 0 , 7378 = 0 , 643

Onde, da Tabela 12.1, com λ 1 T s =   3   μ m   ×   20 00   K   =   60 00   μ m ⋅ K ,   F 0 - λ T =   0 , 7378 .

Passo 3

A absortividade total da amostra, α , para irradiação do recinto em T e n c =   300   K , é

α = ε 1 F ( 0 → λ 1 T e n c ) + ε 2 1 - F 0 → λ 1 T e n c

α = 0,8 × 0 + 0,2 1 - 0 = 0,200

Onde, da Tabela 12.1, com λ 1 T e n c =   3   μ m   ×   300   K   =   900   μ m ⋅ K ,   F ( 0 - λ T ) =   0 .

O balanço de energia na amostra, por unidade de área é:

E ˙ e n t - E ˙ s a i = 0

α l a s G l a s e r + 2 α G - 2 ε E b T s - q c v ' ' = 0

α l a s G l a s e r + 2 α σ T e n c 4 - 2 ε σ T s 4 - 2 h T s - T ∞ = 0

Reconhecendo que α l a s ( 0,5   μ m )   =   0,8 e substituindo os valores numéricos encontramos,

G l a s e r = 1646   k W / m 2

Resposta

  1. ε = 0,643
  2. α = 0,200
  3. G l a s e r = 1646   k W / m 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é efeito da radiação? Como esse efeito influencia as medições de temperatura?
Dê exemplos de efeito da radiação que afeta o conforto humano.
Repita o problema 13-44 substituindo o recinto cúbico por um recinto esférico de 3 m de diâmetro.
Considere uma churrasqueira circular com 0,3 m de diâmetro. O fundo da churrasqueira é coberto com pedaços de carvão quente a 950 K, enquanto a tela metálica em cima dela é incialmente coberta com bif
Considere um forno hemisférico de diâmetro D = 5 m com base plana. A cúpula do forno é negra, e a base tem emissividade de 0,7. A base e a cúpula do forno são mantidas a temperaturas uniformes de 400