Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 93

Uma amostra muito pequena de uma superfície opaca encontra-se inicialmente a 1200   K e tem a absortividade hemisférica espectral mostrada na figura.

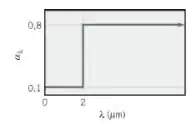
A amostra é colocada no interior de um grande compartimento cujas paredes têm uma emissividade de 0,2 e são mantidas a 2400   K .

(a) Qual é a absortividade hemisférica total da superfície da amostra?

(b) Qual é sua emissividade hemisférica total?

(c) Quais são os valores da absortividade e da emissividade após a amostra permanecer no interior do compartimento por um longo período de tempo?

(d) Para uma amostra esférica com diâmetro de 10   m m em um compartimento no interior do qual há vácuo, calcule e represente graficamente a variação da temperatura da amostra com o tempo, à medida que ela é aquecida partindo de sua temperatura inicial de 1200   K .

Passo 1

Bora ver o que o enunciado está nos dando?! Nessa questão nós temos uma superfície pequena e opaca inicialmente a 1200   K com distribuição α λ prescrita colocada em um gabinete grande a 2400   K .

Com isso vamos encontrar a absortividade hemisférica total da superfície da amostra, a emissividade hemisférica total,   α e ε após um longo período de tempo.

Passo 2

Para resolver essa questão vamos assumir que a superfície é difusamente irradiada e que o gabinete é muito maior que a superfície e a uma temperatura uniforme.

A absortividade hemisférica total é descrita por,

G λ = E λ , b ( T s u r )

Ou seja, a irradiação corresponde à potência emissiva espectral de um corpo negro na temperatura do recinto e é independente da emissividade do recinto.

α = ∫ 0 ∞ α λ G λ d λ ∫ 0 ∞ G λ d λ = ∫ 0 ∞ α λ E λ , b ( λ , T s u r ) d λ E b ( T s u r )

α = α 1 ∫ 0 2 μ m E λ , b ( λ , T s u r ) d λ σ T s u r 4 + α 2 ∫ 2 μ m ∞ E λ , b ( λ , T s u r ) d λ σ T s u r 4

α = α 1 F ( 0 → 2 μ m ) + α 2 1 - F 0 → 2 μ m = 0,1 × 0,6076 + 0,8 1 - 0,6076 = 0,375

Usando a tabela 12.1 para λ   T = 2 × 2400 = 4 8 00 μ m . K ,   F ( 0 → 2 μ m ) = 0,6076

Passo 3

A emissividade hemisférica total é,

ε = ∫ 0 ∞ ε λ E λ , b λ , T s d λ ∫ 0 ∞ E λ , b λ , T s d λ

Como a superfície é difusa,   ε λ =   α λ e a integral podem ser expressos como,

ε = α 1 ∫ 0 2 μ m E λ , b ( λ , T s ) d λ σ T s 4 + α 2 ∫ 2 μ m ∞ E λ , b ( λ , T s ) d λ σ T s 4

ε = α 1 F ( 0 → 2 μ m ) + α 2 1 - F 0 → 2 μ m = 0,1 × 0 , 1403 + 0,8 1 - 0,1403 = 0 , 702

Usando a tabela 12.1 para λ   T = 2 × 12 00 = 24 00 μ m . K ,   F ( 0 → 2 μ m ) = 0 , 1403

Após um longo período de tempo, a superfície estará à temperatura do gabinete. Essa condição de equilíbrio térmico é descrita pela lei de Kirchoff, para a qual,

ε = α = 0,375

Resposta

  1. α = 0,375
  2. ε = 0,702
  3. ε = α = 0,375
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Cinco folhas finas de alumínio idênticas, com emissividade de 0,1 em ambos os lados, são colocadas entre duas placas paralelas muito grandes que têm as temperaturas mantidas uniformes a T 1 = 800K e T
60 – Referindo para a distribuição da transmissividade espectral de um vidro com baixo ferro (Fig. 12.23), descreva brevemente o que significa o “efeito estufa”. Isto é, como o vidro influencia a tran
91 – A radiação solar incidente na superfície da Terra pode ser dividido em componentes direto e difusivo no Problema 12.90. Considere condições para um dia na qual a intensidade da radiação solar dir
97 – Irradiação da superfície da terra da atmosfera exibe uma variação espectral forte, principalmente associado com a janela atmosférica na Seção 12.9.2.A) Para uma faixa 0 ≤ λ ≤ 8 μm a emissividade
Ao analisar o desempenho de um sistema térmico, o engenheiro tem que ser capaz de identificar os processos de transferência de calor relevantes. Somente então o comportamento do sistema pode ser devid