Exercícios de Radiação entre Superfícies - Lista de Exercícios Resolvida

(Adaptado) Um anel com de raio interno e de raio externo é uma peça de aquecimento por radiação de um plano em formato de disco de de raio paralelo ao anel a uma distância de .

Toda uma região que fecha o sistema (forma uma cavidade fechada) é formada de um material que isola o sistema, ou seja, por uma superfície reirradiante.

Sabendo que o anel está a e emite radiação como um corpo negro e que o disco inferior está a e é um corpo cinza e difuso que possui uma emissividade de , determine qual o fluxo de calor radiante entre o disco e o anel.

A parede de um forno industrial é composta por duas paredes planas verticais distantes e com ar (a ) entre elas. As paredes têm altura igual a e largura igual a . A temperatura da parede 1 é mantida a , e a da parede 2 é mantida a .

A emissividade da parede 1 é igual a e a da parede 2, . Considere as paredes como superfícies cinzas difusas e calcule:

O coeficiente de troca de calor por convecção na parede 1, assumindo que a parede 2 não perturba o escoamento próximo a parede 1.

O calor total perdido pela parede 1.

Considere as seguintes propriedades para o ar: .

Oxigênio líquido é armazenado em um vaso esférico com parede delgada e de diâmetro, que está encerrado no interior de um segundo vaso esférico, também com parede delgada e com de diâmetro.

As superfícies dos vasos são cinza, difusas e opacas, com uma emissividade de e são separadas por um espaço no qual há vácuo.

Se a superfície externa está a e a superfície interna está a , qual é a taxa mássica de perda de oxigênio devido à evaporação?

Obs.: O calor latente de vaporização do oxigênio é de .

Em uma plataforma espacial, duas placas de mesmo tamanho são paralelas e estão separadas de . Uma das placas está na temperatura de e a outra na temperatura de .

Essas placas não sofrem incidência solar e o ambiente ao seu redor encontra-se na temperatura de . Para a troca de calor por radiação, o ambiente pode ser representado como uma superfície fictícia, unindo as duas placas e formando a cavidade na forma de um paralelepípedo que é mostrada abaixo.

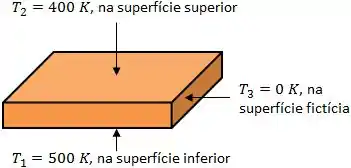
Todas as superfícies são negras. Qual o fluxo de calor por radiação em cada uma das superfícies?

Considere uma sala de 2 metros de altura e uma base quadrada de de lado. Um quadro formado por uma placa aquecedora (A) quadrada de de lado está com sua base a do chão pendurado na parede.

No chão, foi instalada outra placa aquecedora (B) também quadrada de de lado. Todas as demais faces expostas da sala são rerradiantes e forma-se uma cavidade fechada com vácuo no seu interior.

Sabendo que a placa aquecedora (A) tem uma emissividade igual a da placa (B), sendo o valor igual a 0, 4 e considerando que a placa (A) está a e a placa (B) a , determine a taxa de troca de calor entre as placas (A) e (B)

Uma pirâmide tradicional (base quadrada) é utilizada para aquecer objetos colocada no centro da placa da base. As faces triangulares da pirâmide estão a e a base está a .

Qual a quantidade de calor trocada entre a pirâmide e a sua base, considerando apenas a radiação térmica e que as superfícies possuem, respectivamente, emissividade térmica de e ? A base da pirâmide é quadrada com 1,4 metros em cada lado e a altura é de 2,5 metros.

Caracterize analiticamente, provando suas conclusões passo-a-passo, o fator de forma entre a superfície 1 e 2, escrevendo esse fator de forma em função de fatores elementares de forma que esses possam ser encontrados em figuras ou tabelas.

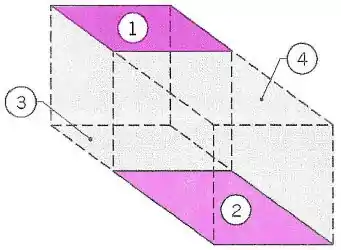
Determine também qual a transferência de calor entre 1 e 2, assumindo que em 1 a temperatura seja de e em 2 a temperatura seja de , sabendo que ambas as superfícies são aço inoxidável, típico, polido. Sabendo também que o meio interno a essa superfície é composto por vácuo.

Considere uma longa fenda em forma de com profundidade de , usinada em um bloco mantida a .

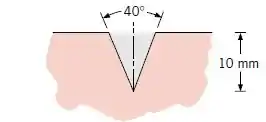
Se as superfícies da fenda são difusas e cinza com uma emissividade de , determine o fluxo radiante que deixa a fenda para a sua vizinhança. Determine também a emissividade efetiva da cavidade.

Considere duas placas paralelas muito grandes com superfícies cinza e difusas.

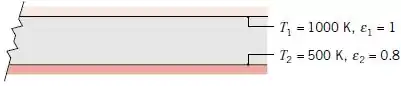
Determine a irradiação na placa superior.

Determine a radiosidade na placa superior.

Qual é a radiosidade da placa inferior.

Qual é a troca líquida de radiação entre as placas por unidade de área das placas?

Considere duas grandes superfícies paralelas, cinza e difusas, separadas por uma pequena distância.

Se a emissividade das superfícies é de , qual deve ser a emissividade de uma barreira de radiação delgada para reduzir a taxa de transferência de calor por radiação entre as duas superfícies por um fator de 10?

Um condutor elétrico muito longo, com de diâmetro, está posicionado concentricamente no interior de um tubo cilíndrico resfriado, com de diâmetro, cuja superfície é difusa e cinza com uma emissividade de e está à temperatura de .

O condutor elétrico possui uma superfície difusa e cinza com uma emissividade de e está dissipando por metro de comprimento.

Considerando que há vácuo no espaço entre as duas superfícies, calcule a temperatura na superfície do condutor.

Para melhorar o descarte de calor em espaçonaves, um engenheiro propõe fixar uma série de aletas retangulares à superfície externa da espaçonave e cobrir todas as superfícies com um material que se aproxima de um comportamento de corpo negro.

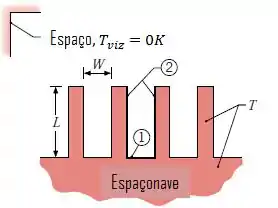
Para superfícies isotérmicas com temperaturas e emissividade , e uma seção em com largura e comprimento , determine a taxa, por unidade de comprimento (normal à página), na qual radiação é transferida de uma seção para o espaço.

(Adaptado) Uma sala de de lado contém duas placas identificadas como 1 e 2 na figura abaixo.

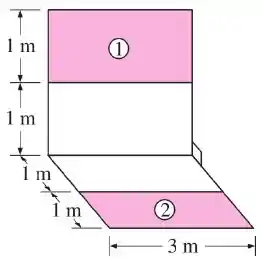
As demais faces da sala são reirradiantes. Sabendo que a placa 1 está a e emite radiação como um corpo negro e que a placa 2 está a e é um corpo cinza e difuso que possui uma emissividade de , determine:

provando matematicamente, quais os fatores de forma associados ao sistema.

o fluxo de calor radiante entre as placas 1 e 2.

Uma barreira de radiação difusa e cinza, com de diâmetro e emissividade e nas superfícies interna e externa, respectivamente, é concêntrica a um longo tubo que transporta um fluido de processo quente.

A superfície do tubo é negra e possui diâmetro de . Há vácuo na região interna da barreira. A superfície externa da barreira está exposta a uma grande sala, cujas paredes estão a , e experimenta transferência de calor por convecção com o ar a , com um coeficiente convectivo de .

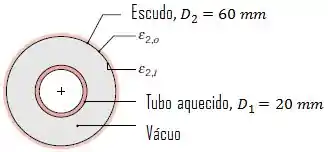
Determine a temperatura de operação do tubo interno se a temperatura da barreira for mantida a .

No fundo de uma grande câmara de vácuo cujas paredes estão a , um painel negro com de diâmetro é mantido a .

Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesmo diâmetro e uma emissividade de é colocada muito próximo ao painel.

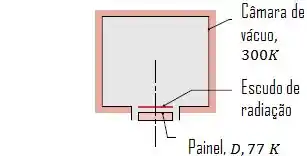
Calcule o ganho líquido de calor no painel.