Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo 1.Exercício - Ex. 13

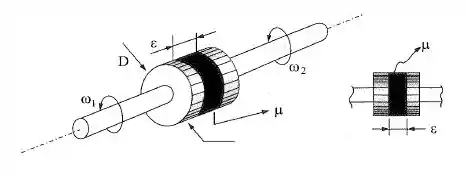
Dois discos são dispostos coaxialmente face a face, separados por um filme de óleo lubrificante de espessura ε pequena. Aplicando-se um momento no disco 1 , ele inicia um movimento em torno de seu eixo e, através do fluido viscoso, estabelece-se o regime, de forma que as velocidades angulares ω 1 e ω 2 ficam constantes. Admitindo o regime estabelecido, determinar a função ω 1 - ω 2 = f M ∀ ε , D , μ .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Queremos uma função f M ∀ ε , D , μ que represente ω 1 - ω 2 . Podemos representar a equação para o momento como:

d M = τ d A

d M = μ v 1 - v 2 ε 2 π ⋅ r ⋅ d r ⋅ r

d M = μ ω 1 - ω 2 r ε 2 π ⋅ r ⋅ d r ⋅ r

Desenvolvendo, temos que:

d M = μ ω 1 - ω 2 ε 2 π ⋅ r 3 ⋅ d r

Passo 2

Descoberta esta relação, podemos integrar a equação nos intervalos do sistema. Observe:

∫ 0 M t d M = ∫ 0 R μ ω 1 - ω 2 ε 2 π ⋅ r 3 ⋅ d r

Resolvendo, temos que:

M t = μ ω 1 - ω 2 ε 2 π R 4 4

Passo 3

Agora podemos representar a função solicitada:

ω 1 - ω 2 = 4 M t ε μ 2 π R 4

Como no enunciado a função deve estar em relação ao diâmetro e R = D 2 , temos que:

R 4 = D 2 4

R 4 = D 4 16

Substituindo, temos que:

ω 1 - ω 2 = 32 M t ε μ π D 4

Resposta

ω 1 - ω 2 = 32 M t ε μ π D 4

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o número de Reynolds da água a 20°C escoando a 0,25 m/s através de tubo de diâmetro 5 mm? Se agora o tubo for aquecido, a que temperatura média da água irá ocorrer a transição do escoamento par
De acordo com Folsom [6], a elevação capilar Δh (mm) de uma interface água­ar em um tubo é correlacionada pela seguinte expressão empírica: Δ h=A e - b D noqualD(mm)éodiâmetrodotubo,A=0,400eb=4,37.Voc
Operfildevelocidadedacamada­limiteviscosa,mostradonaFig.2.15,podeseraproximadoporumaequaçãoparabólica:Acondiçãolimiteéu=U(avelocidadedacorrentelivre)nabordalimiteθ(ondeoatritoviscososetornazero).Deter
Em um processo da indústria de alimentos, tetracloreto de carbono a 20°C escoa através de um bocal cônico de um diâmetro de entrada De = 50 mm para um diâmetro de saída Ds. A área varia linearmente co
Umhidroaviãovoaa160km/hatravésdoara7ºC.Aquedistânciadabordadeataquedoladoinferiordafuselagema camadalimitedevepassardoregimelaminarparaturbulento?Comoessatransiçãodoregimedacamada­limitemudaconformeo