Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 125
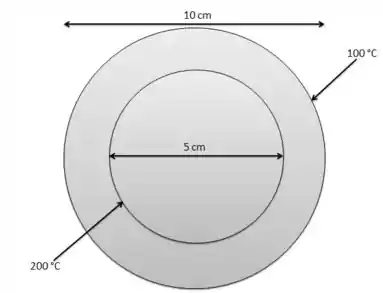
Duas esferas concêntricas com raios de 5 cm e 10 cm estão tendo as temperaturas de superfície mantidas a 200°C e 100°C, respectivamente. O espaço entre as duas superfícies esféricas concêntricas é preenchido com gás nitrogênio a 1 atm. Se ambas as superfícies das esferas concêntricas são pretas ( 1), determine a taxa de transferência de calor na superfície interna.
Passo 1
Então, basicamente temos duas esferas com nitrogênio entre elas e queremos determinar a taxa de transferência de calor da menor para a maior. Sabemos que as temperaturas são 200°C e 100°C e que a emissividade é 1.
Vamos então determinar a perda de calor por convecção e radiação e, no final, a soma deles é a taxa total de transferência que o exercício pede. Pronto? Vamos lá!!!
Passo 2
Como primeiro passo vamos determinar a temperatura de filme do nitrogênio. Para este caso:
Para esta temperatura as propriedades do nitrogênio são:
Podemos então começar a calcular a taxa de transferência por convecção natural. Ela é calculada por:
Então, ainda precisamos da condutividade térmica efetiva. Podemos encontrá-la da seguinte forma:
Em que é o fator geométrico da esfera:
Portanto, vamos primeiro calcular ; depois e por fim, . Vamos lá?
Antes de calcular vamos determinar o número de Rayleigh:
Agora :
Substituindo estes valores na equação da taxa de transferência:
Passo 3
Resta ainda determinar o calor transferido por radiação. Para um espaço entre duas superfícies:
Para o nosso exercício . Então:
Portanto, a taxa de transferência na superfície interna é:
Resposta
A taxa transferida pela superfície interna é .