Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 7

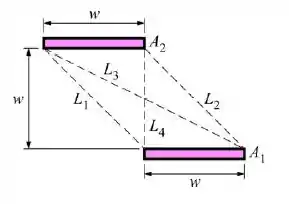
Duas placas paralelas infinitamente longas de largura w são separadas por uma distância w, como mostrado abaixo. Usando o método de linhas cruzadas de Hottel, determine o fator de forma F12.

Passo 1

Vamos usar a dica que ele está nos falando, beleza?

F i → j = ∑ L i n h a s   c r u z a d a s - ∑ L i n h a s   n ã o   c r u z a d a s 2   l i n h a s   n a   s u p e r f í c i e   i

Passo 2

Para as linhas não cruzadas, temos o seguinte:

L 1 = L 2 = w 2 + w 2 1 2 = 2 w 2 1 2 = 2 w

Enquanto para as linhas cruzadas...

L 3 = w 2 + 4 w 2 1 2 = 5 w

Onde L4 = w

Passo 3

Vamos aplicar o método, se liga!!!

F 12 = L 3 + L 4 - ( L 1 + L 2 ) 2 w = 5 w + w - ( 2 w + 2 w ) 2 w = 0,2

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

113 - Dois discos paralelos concêntricos, 20c m e 40c m de diâmetro são separados por uma distância de 10c m .O disco menor ( ε = 0,80 ) se encontra a uma temperatura de 300° C .O disco maior ε = 0,60
Considere um forno hemisférico com uma base circular plana de diâmetro D. Determine o fator de forma da cúpula desse forno até sua base.
Três cilindros paralelos infinitamente longos, de diâmetro D, estão localizados a uma distância s um do outro. Determine o fator forma entre o cilindro do meio e o do entorno.
Considere uma superfície cilíndrica e um disco orientado coaxialmente, como mostrado na Fig. 13-19. O cilindro tem um diâmetro D e um comprimento L. O disco de diâmetro D é colocado coaxialmente com o
Determine os quatro fatores de formas associados a um recinto formado por dois cilindros concêntricos muito longos de raios r 1er 2 . Despreze os efeitos das extremidades.