Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 13.Problemas - Ex. 19
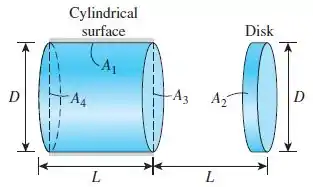
Considere uma superfície cilíndrica e um disco orientado coaxialmente, como mostrado na Fig. 13-19. O cilindro tem um diâmetro D e um comprimento L. O disco de diâmetro D é colocado coaxialmente com o cilindro a uma distância L. Se , determine o fator de vista entre a superfície cilíndrica (1) e o disco (2) faceando-a.
Passo 1
Vamos continuando turminhaaa!!
Animadíssimos?! Espero que sim :P
Bom, se nós queremos o fator de forma , ou seja, a superfície cilíndrica em relação ao disco nós podemos começar usando o somatório com relação a superfície 2, ok?
Sabemos que:
Reorganizando:
Então nosso objetivo aqui é achar , ok? E em seguida usaremos a regra da reciprocidade
Como nós temos superfícies finitas, os fatores de forma podemos ser calculados pela equação:
Se:
E lembrando que:
Então:
No fator de forma:
Passo 2
Como nós temos superfícies finitas, os fatores de forma podemos ser calculados pela equação abaixo, igual a anterior:
Se:
Se nós temos uma distância de 2L entre as superfícies:
Então:
No fator de forma:
Passo 3
Colocando nossos dados na fórmula do Passo 1:
Agora só precisamos da regra da reciprocidade:
A área nós já podemos calcular:
Se:
Então:
Colocando no fator de forma:
Substituindo:
Finalizamos mais uma galerinha !!