Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 90

Durante uma experiência, três bolas de alumínio (ρs = 2600 kg/m³) com diâmetros de 2,4 e 10 mm, respectivamente, são jogadas em um tanque cheio com glicerina a 22°C (ρf = 1274 kg/m³ e μ = 1 kg/m.s). As velocidades terminais de descida das bolas são medidas resultando em 3,2, 12,8 e 60,4 mm/s, respectivamente. Compare esses valores com as velocidades previstas pela lei de Stokes para a força de arrasto FD = 3πμDV, que é válida para números de Reynolds muito baixos (Re

Passo 1

Faaaaaaaaaaaaaala galera, tudo bem? Vem comigo pra gente analisar esse enunciado e resolver esse problema juntos!

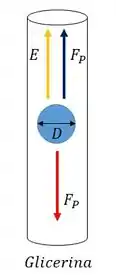
Nesse problema a gente tem três bolas de alumínio de diâmetros diferentes (2, 4 e 10 m m ), que são jogadas em um tanque com glicerina, como mostra o esquema ilustrativo abaixo:

Mas aí você se pergunta “o que a gente tem que fazer pra resolver essa questão????”.

Bem, nosso objetivo final é calcular a velocidade terminal pra cada uma das esferas e comparar com as velocidades terminais medidas experimentalmente, que são respectivamente de 3,2, 12,8 e 60,4 m m / s .

Pra isso, a gente tem que entender que a força de arrasto F D nesse problema pode ser calculada como a diferença entre a força peso da bolinha F P e o empuxo E aplicado pelo fluido. Ou seja:

F D = F P - E

Por isso, a gente tem que utilizar a chamada Lei de Stokes utilizada para quedas de pequenas esferas, dada pela seguinte equação:

F D = 3 π μ V t D

Mas fique atento! Essa suposição só é válida quando o número de Reynolds bem pequenos com R e ≪ 1 . Então, depois de calcular a velocidade a gente vai checar se esse fato é válido pra cada uma situação!

Além disso, devemos calcular a força peso e o empuxo a partir das equações abaixo:

F P = ρ s g V     e   E = ρ f g V  

Sendo g = 9,81   m 2 / s a aceleração da gravidade e V = π D ³ 6 o volume da esfera lançada no fluido.

Antes da gente ir pros próximos passos, guarde as seguintes propriedades que vamos utilizar nos próximos passos:

μ = 1 k g m ∙ s ρ s = 2600 k g m 3 ρ f = 1274 k g m ³

Pronto, agora que a gente já analisou esse enunciado e entendemos o que temos que fazer, já podemos partir pra encarar esse problema!

Passo 2

Vamo começar deduzindo uma expressão pra calcular a velocidade terminal do fluido a partir do balanço de forças que eu te mostrei no Passo 1:

F D = F P - E → 3 π μ V t D = ρ s g V - ρ f g V      

Reorganizando a equação e explicitando V t :

V t = ρ s - ρ f g V 3 π μ D

Agora vamos calcular a velocidade para cada uma das bolinhas de diferentes diâmetros:

  1. Para D = 2   m m :

    2. V t = 2600 k g m 3 - 1274 k g m ³ 9,81   m 2 / s π 0,002   m ³ 6 3 π 1 k g m ∙ s 0,002   m

    → V t = 0,00289   m s = 2,89   m m s

  2. Para D = 4   m m :

    3. V t = 2600 k g m 3 - 1274 k g m ³ 9,81   m 2 / s π 0,004   m ³ 6 3 π 1 k g m ∙ s 0,004   m

    → V t = 0,01156   m s = 11,56   m m s

  3. Para D = 10   m m :

V t = 2600 k g m 3 - 1274 k g m ³ 9,81   m 2 / s π 0,010   m ³ 6 3 π 1 k g m ∙ s 0,010   m

→ V t = 0,07227   m s = 72,27   m m s

Passo 3

Vamo agora calcular o erro pra cada uma das velocidades que a gente calculou no passo anterior com relação às velocidades medidas experimentalmente:

  1. Para D = 2   m m ( V t , e x p = 3,2   m m / s )

    2. E r r o 1 = V t , e x p - V t V t , e x p × 100 % = 3,2 m m s - 2,89   m m s 3,2   m m s × 100 %

    E r r o 1 = 9,69 %

  2. Para D = 4   m m ( V t , e x p = 12,8   m m / s ):

    3. E r r o 2 = V t , e x p - V t V t , e x p × 100 % = 12,8 m m s - 11,56   m m s 12,8   m m s × 100 %

    E r r o 2 = 9,69 %

  3. Para D = 10   m m ( V t , e x p = 60,4   m m / s ):

E r r o 3 = V t - V t , e x p V t , e x p × 100 % = 60,4 m m s - 72,27   m m s 60,4   m m s × 100 %

E r r o 3 = 19,65 %

Como dá pra perceber, os erros pras velocidades terminais das duas primeiras esferas são menores que 10 % , erro considerado baixo para aplicações de engenharia, dentro do tolerado.

Já pra terceira bolinha, o erro é de quase 20 % , fora do tolerado, demonstrando que a Lei de Stokes não modela bem a queda dessa esfera na glicerina.

Passo 4

Pra finalizar a questão, vamos calcular os números de Reynolds com as velocidades terminais calculadas no Passo 2 a fim de testar se eles estão na faixa para a qual podemos aplicar a Lei de Stokes:

  1. Para D = 2   m m ( V t = 2,89   m m / s )

    2. R e 1 = ρ f V t D μ = 1274 k g m 3 0,00289 m s 0,002   m 1 k g m ∙ s = 0,0074

  2. Para D = 4   m m ( V t , = 11,56   m m / s ):

    3. R e 2 = ρ f V t D μ = 1274 k g m 3 0,01156 m s 0,004   m 1 k g m ∙ s = 0,059

  3. Para D = 10   m m ( V t = 72,27   m m / s ):

R e 3 = ρ f V t D μ = 1274 k g m 3 0,07227 m s 0,010   m 1 k g m ∙ s = 0,9207

A gente consegue notar que os números de Reynolds para as duas primeiras esferas estão dentro da ordem de grandeza em que podemos utilizar a Lei de Stokes.

Já para a terceira esfera, o número de Reynolds está muito perto de 1 e já foge da faixa de aplicação da Lei de Stokes. Isso ajuda a explicar por que o erro que a gente calculou pra velocidade terminal dessa esfera foi tão grande!

UFA, finalmente finalizamos essa questão juntos!

Resposta

As velocidades terminais calculadas pra cada uma das esferas são, respectivamente: 2,89 , 11,56 e 72,27   m m / s .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Bolas Wiffle TM, feitas de plástico leve com vários furos são usadas para praticar beisebol e golfe. Explique os propósitos dos furos e como eles funcionam. Explique como você verificaria suas hipótes
Por que é possível lançar uma bola de futebol americano mais facilmente em um movimento espiral do que em um movimento de rotação da bola em torno das suas extremidades?
O professor instrutor dos alunos do projeto do aeroplano do Problema 9.163 não está satisfeito com a ideia de usar folha rígida de plástico para o aerofólio. Ele solicita aos estudantes que avaliem a
Um aeroplano leve, com massa M = 1000k g , tem uma seção convencional (NACA 23015) de asa de área planiforme A = 10m 2 . Determine o ângulo de ataque da asa para uma velocidade de cruzeiro V = 63m / s
Um objeto cai no ar no interior de um longo duto vertical. A velocidade do objeto é constante em 3m / s . A configuração do escoamento em volta do objeto é mostrada. A pressão estática é uniforme nas