Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 11.Problemas - Ex. 83
Um painel de anúncio retangular de 2 m de altura e 4 m de largura está preso a um bloco de concreto de 4 m de largura e 0,15 m de altura (densidade = 2300 kg/m³) por dois mastros de 5 cm de diâmetro, 4 m de altura (parte exposta), como mostra a Figura P11-83. Se o anúncio deve resistir a ventos de 150 km/h de qualquer direção, determine (a) a máxima força de arrasto no painel, (b) a força de arrasto que age nos mastros e (c) o comprimento mínimo L do bloco de concreto para que o painel resista aos ventos. Considere a densidade do ar como 1,30 kg/m³.
Passo 1
Faaaaaaaaaaaaaala galera, tudo bem? Vem comigo pra gente analisar esse enunciado e resolver esse problema juntos!
Nesse problema a gente tem um painel de anúncio retangular preso a um bloco de concreto por dois mastros, expostos a ventos de () e densidade , como mostra o esquema ilustrativo abaixo, com todas as grandezas que vamos utilizar na resolução:
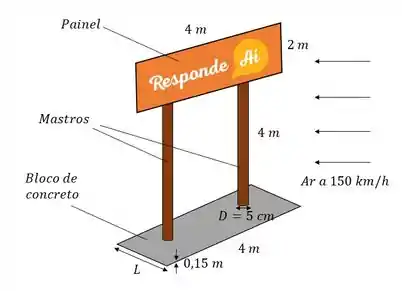
Mas aí você se pergunta “o que a gente tem que fazer pra resolver essa questão????”.
Bem, nosso objetivo final é fazer um balanço de momento no bloco de concreto e calcular o comprimento mínimo para que o painel resista aos ventos.
Maaaaaaaas, pra isso, a gente tem que calcular a força de arrasto máxima agindo tanto no painel de anúncio quanto nos mastros. Essa força de arrasto máxima vai ser alcançada quando a gente considerar um escoamento normal ao painel.
Pra fazer isso, a gente tem que utilizar a seguinte equação pra força de arrasto em um corpo submerso:
Sendo a área frontal do corpo a massa específica do ar, a velocidade do ar e o coeficiente de arrasto do corpo.
Pronto, agora que a gente já analisou esse enunciado e entendemos o que temos que fazer, já podemos partir pra encarar esse problema!
Passo 2
Vamo começar então resolvendo a letra (a) e calculando a força de arrasto pro painel de anúncio. Mas pra isso, antes a gente tem que buscar o coeficiente de arrasto .
Tanto no enunciado quanto no nosso esquema ilustrativo, a gente viu que a velocidade do ar é , que é uma velocidade muito alta. Sendo assim, a gente pode considerar que o ar escoa em regime turbulento.
Por isso, a gente pode ir na Tabela 11-1 (página 501), e buscar o coeficiente de arrasto pra uma barra retangular de comprimento , que corresponde a uma placa fina, que é o nosso caso nesse problema.
Nessa tabela, encontramos então . Considerando a área superficial do painel como sendo , e substituindo as propriedades dadas no enunciado e no Passo 1, temos que a força de arrasto é:
Passo 3
Agora, a gente vai pra letra (b) calcular a força de arrasto nos dois mastros, cuja área frontal é .
Novamente, a velocidade do vento faz com que o escoamento seja turbulento, e se a gente for na Tabela 11-1, descobrimos que o coeficiente de arrasto pra uma haste circular submetida a um escoamento turbulento é .
Agora a gente vai usar a mesma equação descrita no Passo 1 pra calcular o coeficiente de arrasto para os mastros. MAS PERA LÁ! A gente tem que lembrar que como são dois mastros, nossa equação vai ter que ser multiplicada por 2:
Passo 4
Pra finalizar a questão, a gente vai resolver a letra (c) pra calcularmos o comprimento mínimo do bloco pra aguentar a força do vento.
Antes de tudo, a gente tem que calcular a força peso exercida em todo o volume do bloco de concreto de densidade :
E deixamos a força peso em função de , que é o que queremos descobrir.
Vamo agora fazer o balanço de momento. A gente tem que lembrar que o momento é uma força aplicada em uma distância. Pro caso das forças de arrasto, o momento será calculado levando em conta todas medidas frontais.
Já pra força peso, o momento será avaliado no centro de gravidade do bloco de concreto ().
Sendo assim, vamos fazer o balanço de momento, lembrando que ele deve ser zero para que o painel resista em pé à força do vento:
Substituindo os valores que calculamos pra todas essas forças:
Reorganizando e resolvendo a equação pra :
Agora sim, terminamos de matar a questão juntos!
Resposta
(a) A máxima força de arrasto no painel é .
(b) A força de arrasto que age nos mastros é .
(c) O comprimento mínimo L do bloco de concreto para que o painel resista aos ventos é .