Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 12.Problemas - Ex. 90
Qual é o efeito do aquecimento do fluido sobre a velocidade do escoamento no escoamento subsônico de Rayleigh? Responda a mesma pergunta para o escoamento supersônico de Rayleigh.
Passo 1
O enunciado faz duas perguntas pra gente. Para saber quais são essas duas perguntas temos que lembrar que o escoamento de Rayleigh é o escoamento de um gás ideal que troca calor ao longo de um duto. A figura abaixo mostra esse escoamento. Nós vemos que o fluido antes de ser aquecido possui uma velocidade e um número de Mach . Depois de ser aquecido, o fluido passa a ter uma velocidade e um número de Mach .
Com essa figura fica
- O que acontece com a velocidade de um gás escoando com velocidade subsônica (velocidade menor que a velocidade do som e número de Mach menor que 1), quando ele é aquecido? Ou seja, é maior, menor ou igual a ?
- O que acontece com a velocidade de um gás escoando com velocidade supersônica (velocidade maior que a velocidade do som e número de Mach maior que 1), quando ele é aquecido? Ou seja, é maior, menor ou igual a ?
Para estudar escoamento de Rayleigh e descobrir o efeito do aquecimento sobre , usamos um gráfico T-s (temperatura versus entropia) como mostrado abaixo. A curva do gráfico T-s é chamada de linha de Rayleigh.
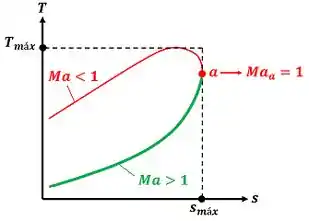
A linha verde é usada para escoamentos supersônicos e a linha vermelha é usada para escoamentos subsônicos.
O ponto “a” da linha de Rayleigh é o ponto de maior entropia . O número de Mach do ponto “a” vale .
Passo 2
Neste passo vamos descobrir o efeito do aquecimento sobre a velocidade de um fluido em escoamento subsônico .
Como a entropia de um escoamento subsônico aumenta quando ele é aquecido, a tendência do fluido é caminhar para a direita até alcançar o ponto “a”. Logo, a tendência do seu número de Mach é aumentar de para do ponto “a”.
Como o número de Mach era menor que 1 e tende a ser igual a 1, aumenta.
Além disso, a fórmula do número de Mach é:
Ou seja, como o número de Mach é proporcional à velocidade do fluido, quando aumenta, aumenta.
Logo, a velocidade do fluido aumenta com o aquecimento, quando o escoamento é subsônico! Ou seja, fica maior que .
Passo 3
Neste passo vamos descobrir o efeito do aquecimento sobre a velocidade de um fluido em escoamento supersônico .
Como a entropia de um escoamento supersônico aumenta quando ele é aquecido, a tendência do fluido é caminhar para a direita até alcançar o ponto “a”. Logo, a tendência do seu número de Mach é diminuir de para do ponto “a”.
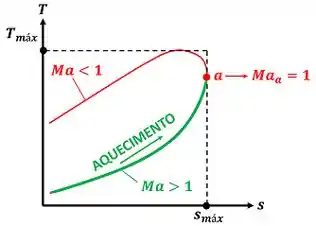
Como o número de Mach era maior que 1 e tende a ser igual a 1, diminui.
Além disso, a fórmula do número de Mach é:
Ou seja, como o número de Mach é proporcional à velocidade do fluido, quando diminui, diminui.
Logo, a velocidade do fluido diminui com o aquecimento, quando o escoamento é supersônico! Ou seja, fica menor que .
Resposta
A velocidade do fluido aumenta com o aquecimento, quando o escoamento é subsônico. A velocidade do fluido diminui com o aquecimento, quando o escoamento é supersônico!