Um elemento aquecedor coberto com níquel, com uma espessura de 15 mm e uma condutividade térmica de 50W /( m · K ) , está exposto à água saturada a pressão atmosférica. Um termopar é fixado à sua superfície posterior, que é bem isolada. 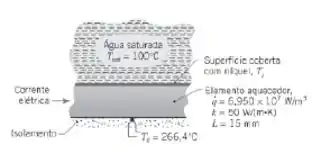Medidas em uma condição de operação particular fornecem uma dissipação de potência elétrica no elemento aquecedor de 6,950 × 10 7W / m 3 e uma temperatura de T o = 266,4 ° C .a) A partir dos dados anteriores, calcule a temperatura da superfície, T s , e o fluxo térmico na superfície exposta.b) Usando o fluxo térmico na superfície determinado na parte a), estime a temperatura da superfície utilizando uma correlação de ebulição apropriada.

a )T s = 383K = 110 ° C q s ' ' = 1,0425 × 10 6W / m 2 b )T s = 109,08 ° C

Enunciado

Letra a)

Temos que distribuição da temperatura, dada à geração de calor, é:

Quando , temos:

Assim:

Dados:

;

Temos:

Calculando o fluxo térmico:

Substituindo os dados:

Letra b)

Calculando o excesso de temperatura:

Dados:

;

Temos:

Pela correlação de Rohsenow, o fluxo de calor é dado por:

Pela Tabela obtemos as seguintes propriedades da água saturada sob :

Para a combinação de fluidos de superfície como níquel e água, o coeficiente de correlação é dado:

Substituindo os dados na equação:

Sabendo que:

Então: