Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 9.Problemas - Ex. 74

No tratamento analítico da aleta com área de seção transversal uniforme foi suposto que o coeficiente de transferência de calor por convecção era constante ao longo do comprimento da aleta. Considere uma aleta de aço A I S I   316 com 6   m m de diâmetro e 50   m m de comprimento (com extremidade isolada), que opera sob as seguintes condições: T b   =   125 ° C , T ∞   =   27 ° C , T v i z   =   27 ° C e ε   =   0,6 .

( a ) Estime valores médios para os coeficientes de transferência de calor por convecção natural ( h c ) e por radiação ( h r ) na aleta. Use esses valores para estimar a temperatura na extremidade da aleta e sua efetividade.

( b ) Utilize um método numérico para estimar os parâmetros anteriores com os coeficientes convectivo e radiante na aleta com base em valores locais, ao invés dos valores médios.

Passo 1

Vamos começar o exercício interpretando sua física, inicialmente do enunciado temos os dados da aleta em questão:

T b   =   125 ° C , T ∞   =   27 ° C , T v i z   =   27 ° C e ε   =   0,6

Além disso, devemos retirar um dado muito importante para a formulação, de que a aleta é adiabática de área de seção uniforme, pois sua extremidade se encontra isolada. Logo:

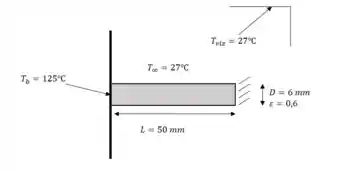
Note que a aleta possui uma emissividade, então temos que ter em mente que teremos a influência de radiação.

Passo 2

Temos que o fluido em questão é o ar. Utilizando a tabela A-4 e a A-1 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.), podemos buscar as supostas propriedades...

Mas antes, precisamos estimar a temperatura de superfície para estimar os parâmetros para a aleta:

T s - = T b + T ∞ 2 = 125 + 27 2 = 77 + 273 = 350   K

k = 14,3 W m ∙ K

Utilizando da temperatura de superfície, podemos estimar a temperatura de filme para entrar na tabela:

T f = T s - + T ∞ 2 = 77 + 27 2 = 52 + 273 = 325   K

υ = 18,41 × 10 - 6 m 2 s ,   k = 0,0282 W m ∙ K ,   α = 26,2 × 10 - 6 m 2 s ,   P r = 0,704

β = 1 T f = 3,077 × 10 - 3 K - 1

Passo 3

Muito bem galera, agora podemos prosseguir com a resolução...

Da questão ( a ) , temos que determinar um valor médio para h - c e h - r , além disso precisamos determinar a efetividade da aleta.

Lembra que nossa aleta é adiabática? Ou seja, sua ponta é isolada de qualquer convecção...

Portanto a formulação será a seguinte:

θ L = θ b ⁡ cosh ⁡ m L - x cosh ⁡ m L      

Como queremos saber a temperatura na ponta da aleta, logo ( x = L ) ...

θ L = θ b cosh ⁡ mL ⁡  

Onde,

θ L = T L - T ∞

θ b = T b - T ∞

Passo 4

Bom, agora seguindo....

Nesse problema, temos que encontrar o coeficiente médio de convecção o que basicamente é:

h - = h - c + h - r

Logo, começando elo primeiro coeficiente, temos que ter em mente que a aleta sofre convecção natural e que se trata de uma aleta de seção circular horizontal, portanto, a correlação correspondente é:

N u - D = h - c D k = C R a D n

R a D = g β ∆ T D 3 υ α = 9,81 m s 2 3,077 × 10 - 3 K - 1 350 - 300 K 0,006   m 3 18,41 × 10 - 6 m 2 s 26,2 × 10 - 6 m 2 s = 675

Temos que C e n se encontram na tabela 9.1 (Incropera - Fundamentos de Transferência de Calor e Massa - 7°Ed.). Portanto:

N u - D = 0,850 675 0,188 = 2,8724

N u - D = h - D k

h - c = 2,8724 0,0282 W m ∙ K 0,006   m = 13,6 W m 2 ∙ K

Passo 5

Partindo para o segundo coeficiente...

h - r = ε σ ( T - s + T v i z ) ( T - s 2 + T v i z 2 )

h - r = 0,6 × 5,67 × 10 - 8 W m 2 ∙ K 4 350 + 300 350 2 + 300 2 K 3 = 4,7 W m 2 ∙ K

Por fim...

h - = h - c + h - r = 13,6 W m 2 ∙ K + 4,7 W m 2 ∙ K = 18,3   W m 2 ∙ K

Passo 6

Voltando para nossas equações iniciais...

θ L = T L - T ∞ = ( T b - T∞ ) cosh ⁡ mL ⁡  

Onde,

P = π D = π × 0,006   m = 1,885 × 10 - 2   m

A c = π D 2 4 = π 0,006   m 2 4 = 2,827 × 10 - 5 m 2

m = h - P k A c 1 2 = 18,3   W m 2 ∙ K 1,885 × 10 - 2   m 14,3 W m ∙ K 2,827 × 10 - 5 m 2 1 2 = 29,21   m - 1

Por fim...

T L - T ∞ = T b - T∞ cosh ⁡ mL ⁡  

T L - 27 = 125 - 27 K cosh ⁡ 29,21   m - 1 × 0,050   m = 43,2   K

T L = 43,2   K + 27 + 273 = 343,2   K

T L = 70,2 ℃

Passo 7

Para concluirmos a questão ( a ) basta determinarmos a efetividade da aleta, ou seja:

ε = q h - A c , b θ b

Onde para aleta adiabática...

q = M ∙ tanh ⁡ ( m L )

M = h - P k A c θ b

Portanto:

M = 18,3 W m 2 ∙ K 1,885 × 10 - 2   m 14,3 W m ∙ K 2,827 × 10 - 5 m 2 125 - 27 K

M = 1,157 W

q = 1,157 W ∙ tanh ⁡ 29,21   m - 1 × 0,050   m = 1,039   W

Por fim...

ε = 1,039   W 18,3 W m 2 ∙ K 2,827 × 10 - 5 m 2 ( 125 - 27 ) K = 20,5

Passo 8

A questão ( b ) pede para utilizar o método numérico para resolução dos mesmos passos anteriores, porém como método numérico será possível discretizar a aleta em elementos nodais.

A partir de um auxílio de um software, a resolução dos elementos nodais trará uma melhor aproximação dos valores finais do exercício anterior.

Resposta

( a ) Valores médios para os coeficientes de transferência de calor por convecção natural ( h c ) e por radiação ( h r ) na aleta:

h - c = 13,6 W m 2 ∙ K

h - r = 4,7 W m 2 ∙ K

Valores para a temperatura na extremidade da aleta e sua efetividade:

T L = 70,2 ℃

ε = 20,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que as superfícies aletadas são frequentemente utilizadas na prática? Por que as superfícies aletadas são chamadas de dissipadores de calor na indústria eletrônica?
Considere a convecção natural laminar em placa vertical quente. O fluxo de calor será mais elevado na parte superior ou inferior da placa? Por quê?
Dissipadores de calor de alumínio com perfil retangular são comumente usados ​​para resfriar componentes eletrônicos. Considere um dissipador de calor de 7,62 cm de comprimento e 9,68 cm de largura cu
Uma placa de 10c m × 10c m tem uma temperatura de superfície constante de 150°C. Determine o número de Grashof se o chip for colocado nos seguintes fluidos: Ar (1 atm, 30°C); Água líquida (30°C);Óleo
Por que dissipadores de calor com aletas estreitamente compactas não são adequados para a transferência de calor por convecção natural, apesar de aumentarem a superfície de transferência de calor?