Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 10.Problemas - Ex. 7

Represente graficamente o fluxo térmico da ebulição nucleada de água saturada a pressão atmosférica sobre uma grande placa horizontal de cobre polido, na faixa de excesso de temperatura de 5 ° C ≤ ∆ T e ≤ 30 ° C . Compare os seus resultados com a Figura 10.4. Também determine o excesso de temperatura correspondente ao fluxo térmico crítico.

Passo 1

Começamos o problema obtendo as seguintes propriedades da água saturada na Tabela A .   6 a 1   a t m :

T s a t = 100 ° C = 373   K

h f g = 2257   k J / k g

ρ v = 0,596   k g / m 3

ρ l = 957,9   k g / m 3

μ l = 279 × 10 - 6   N ⋅ s / m 2

P r L = 1,76

c p , l = 4217   J / k g ⋅ K

σ = 58,9 × 10 - 3   N / m

Passo 2

Pela correlação de Rohsenow obtemos o fluxo térmico da ebulição nucleada:

q s ' ' = μ l h f g g ρ l - ρ v σ 1 2 c p , l ∆ T e C s , f h f g P r n 3

Pela Tabela 10.1:

C s , f = 0,0128   e   n = 1

Sendo:

g = 9,8   m / s 2 .

Temos:

q s ' ' = 279 × 10 - 6 ⋅ 2257 × 10 3 ⋅ 9,8 ⋅ 957,9 - 0,596 58,9 × 10 - 3 1 2 4217 ⋅ ∆ T e 0,0128 ⋅ 2257 × 10 3 ⋅ 1,76 1 3

q s ' ' = 143 ∆ T e 3

Passo 3

Calcularemos o fluxo térmico da ebulição nucleada na faixa de excesso de temperatura de 5 ° C ≤ ∆ T e ≤ 30 ° C .

Com ∆ T e = 5 ° C :

q s ' ' = 143 ⋅ 5 3

q s ' ' = 17875   W / m 2

Com ∆ T e = 10 ° C :

q s ' ' = 143 ⋅ 10 3

q s ' ' = 143000   W / m 2

Com ∆ T e = 15 ° C :

q s ' ' = 143 ⋅ 15 3

q s ' ' = 482625   W / m 2

Com ∆ T e = 20 ° C :

q s ' ' = 143 ⋅ 20 3

q s ' ' = 1144000   W / m 2

Com ∆ T e = 25 ° C :

q s ' ' = 143 ⋅ 25 3

q s ' ' = 2234375   W / m 2

Com ∆ T e = 30 ° C :

q s ' ' = 143 ⋅ 30 3

q s ' ' = 3861000   W / m 2

Passo 4

Tabelando os dados:

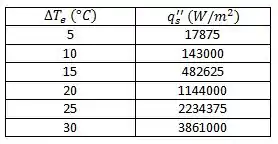
Plotando o gráfico:

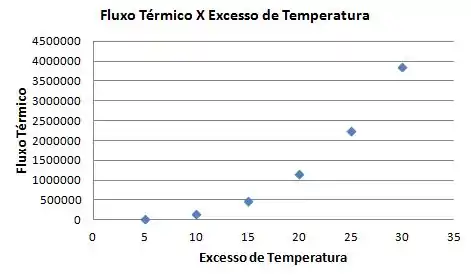
Comparando os valores obtidos com a Figura 10.4, percebendo que a curva se difere, especialmente quando analisamos valores mais altos de excesso de temperatura.

Passo 5

Calculando o excesso de temperatura correspondente ao fluxo térmico crítico:

q s ' ' = q m á x ' '

O Fluxo térmico crítico se dá pela fórmula:

q m á x ' ' = C h f g ρ v σ g ρ l - ρ v ρ v 2 1 4

Pela Tabela 10.1:

C = 0,149

Então, substituindo os dados:

q m á x ' ' = 0,149 ⋅ 2257 × 10 3 ⋅ 0,596 ⋅ 58,9 × 10 - 3 ⋅ 9,8 ⋅ 957,9 - 0,596 0,596 2 1 4

q m á x ' ' = 1258748

Substituindo q m á x ' ' obtido na equação do Passo 2:

1258748 = 143 ∆ T e 3

∆ T e = 20,65 ° C

Resposta

∆ T e = 20,65 ° C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Refaça o exercício anterior, considerando metanol no lugar do benzeno.
O ar com umidade relativa de 80%a35 ° Ce1a t m envolve as faces de uma placa-plana vertical parada de 2,15m de altura, em que ambas as faces estão embutidas por uma fina película aderente de água tamb
Considere uma placa-plana parada de naftaleno de 1m de comprimento por 1m de largura, encontrada em pé em uma parede, sendo que a outra face está em contato com o ar seco. Considerando que haja convec
Refaça os exercícios (9) e (10), considerando:a) t = 50 ° C ; v ∞ = 0,1m / h ;b) t = 50 ° C ; v ∞ = 0,2m / h
Considere um transístor para montagem sobre a superfície de um circuito integrado cuja temperatura é mantida a 35°C. Ar a 20°C escoa sobre a superfície superior, de dimensões 4 mm por 8 mm, com um coe