Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 33

Se T s   ≈   T v i z   na Equação 1.9 , o coeficiente de transferência de calor por radiação pode ser aproximado pela equação

h r , a = 4 ε σ T 3 -

Sendo T - ≡   ( T s   +   T v i z ) / 2 . Desejamos avaliar a validade dessa aproximação através da comparação de valores de h r e h r , a   para as condições a seguir. Em cada caso, represente os seus resultados graficamente e comente sobre a validade da aproximação.

(a) Considere uma superfície de alumínio polido ε   =   0 , 5   ou pintada de preto ( ε   =   0,9 ) ,   cuja temperatura pode exceder a da vizinhança ( T v i z   =   25 ° C )   de   10   a   100 ° C . Compare também os seus resultados com os valores dos coeficientes de transferência associados à convecção natural no ar ( T ∞   =   T v i z ) ,   em que h ( W / ( m 2   ·   K ) )   =   0,98   Δ T 1 3   .

(b) Considere condições iniciais associadas à colocação de uma peça a T s   =   25 ° C   no interior de uma grande fornalha cuja temperatura das paredes pode variar na faixa de 100   ≤   T v i z   ≤   1000 ° C . De acordo com o acabamento ou revestimento da superfície da peça, sua emissividade pode assumir os valores   0,05 ;   0,2   e   0,9 . Para cada emissividade, faça um gráfico do erro relativo, ( h r   -   h r , a     ) / h r , em função da temperatura da fornalha.

Passo 1

Escreva passo aqui Bora para uma questão?! Essa é mais abstrata e nos é fornecido expressões exatas e aproximadas para o coeficiente de radiação linearizado,   h r e h r , a , respectivamente.

A questão quer que a gente compare os coeficientes com diferentes emissividades e temperaturas da superfície. Além disso, temos que fazer um gráfico do erro relativo ( h r   -   h r , a     ) / h r em função da temperatura da fornalha associada a uma peça de T s   =   25   °   C   com ε   = 0,05 ;   0,2   e   0,9 .

Passo 2

Para resolver essa questão, vamos considerar que as paredes da fornalha são grandes em comparação com a peça e estamos em condição de estado estacionário.

O coeficiente de radiação linearizado segue a equação da taxa de troca da radiação da seguinte forma:

h r = ε σ ( T s + T v i z ) (   T s 2 - T v i z 2 )

Se T s   ≈   T v i z , o coeficiente pode ser aproximado pela expressão:

h r , a = 4 ε σ T 3 -

Onde,

T - ≡ T s   +   T v i z 2

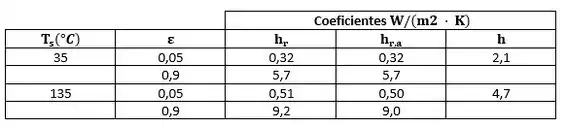
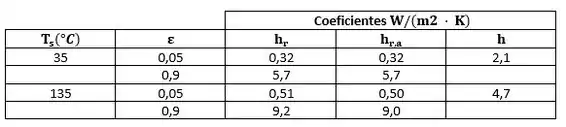
Para a condição de ε   =   0,9 ,   T s = T v i z + 10 = 35 ° C = 308   K e T v i z = 2 5 ° C = 298   K , vemos que:

h r = 4 × 0,05 × 5,67 × 10 - 8 W m 2 . K 4 308 + 298 308 2 - 298 2 K 3 = 0,32   W / m 2

h r , a = 4 × 0,05 × 5,67 × 10 - 8 W m 2 . K 4 308 + 298 2 3 K 3 = 0,32   W / m 2

Para o coeficiente de convecção livre com T s   =   35   °   C   e   T ∞   =   T v i z   =   25   °   C , descobrimos que:

h =   0,98   Δ T 1 3 = 0,98 T s - T ∞ 1 3 = 0,98 308 - 298 1 3 = 2,1 W / m 2 . K  

Para o intervalo T s   -   T v i z   =   10   a   100   °   C   com   ε   =   0,05   e   0,9 , os resultados para os coeficientes são tabelados abaixo. Para esta faixa de temperaturas da superfície e do ambiente, os coeficientes de radiação e convecção livre são de magnitude comparável para valores moderados da emissividade, digamos   ε >   0,2 . A expressão aproximada para o coeficiente de radiação linearizado é válida dentro de 2 %   para essas condições.

Passo 3

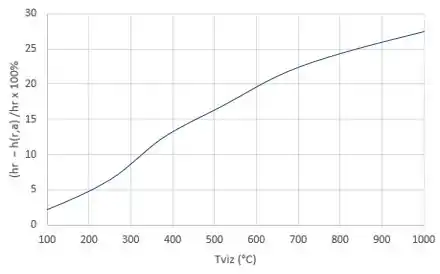
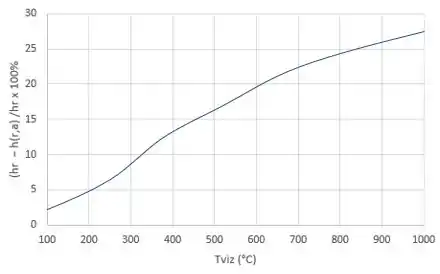
Para a letra (b), nós temos que as expressões acima para os coeficientes de radiação, h r e h r , a , são usadas para a peça a T s   =   2 5   °   C colocada dentro da fornalha com paredes que podem variar de 1 0 0   a   100 0 ° C .

O erro relativo, ( h r   -   h r , a     ) / h r , será independente da emissividade da superfície e é plotado como uma função de T v i z . Para   T v i z >   150   °   C , a expressão aproximada fornece estimativas com erro superior a 5%. Essa expressão aproximada deve ser usada com cautela e apenas para diferenças de temperatura na superfície e nos arredores de 5 0   a   10 0 ° C .

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O que é luz visível? Como ela difere das outras formas de radiação eletromagnética?
O que é radiação térmica? Como ela difere das outras formas de radiação eletromagnética?
Como o cozimento por micro-ondas difere do cozimento convencional?
Qual é a causa da cor? Por que alguns objetos parecem azuis enquanto outros parecem vermelhos? A cor da superfície na temperatura ambiente está relacionada com a radiação que ela emite?
Uma lâmpada incandescente deve emitir pelo menos 15 % de energia em comprimentos de onda mais curtos do que 0,8μ m . Determine a temperatura mínima na qual o filamento da lâmpada deve ser aquecido.