Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 29
Sob condições nas quais a mesma temperatura em um quarto é mantida por um sistema de aquecimento ou resfriamento, não é incomum uma pessoa sentir frio no inverno e estar confortável no verão. Forneça uma explicação razoável para esta situação (apoiada em cálculos), considerando um quarto cuja temperatura ambiente seja mantida a ao longo do ano, enquanto suas paredes encontram-se normalmente a e no verão e no inverno, respectivamente. A superfície exposta de uma pessoa no quarto pode ser considerada a uma temperatura de ao longo do ano, com uma emissividade de . O coeficiente associado à transferência de calor por convecção natural entre a pessoa e o ar do quarto é de aproximadamente
Passo 1
Essa é uma questão de convecção com radiação, beleza? Nós temos as temperaturas do ar e da parede de uma sala, a temperatura da superfície, o coeficiente de convecção e a emissividade de uma pessoa na sala, que nesse caso vai ser o Bart Simpson (hehehe).
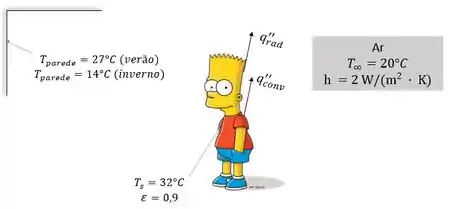
Com essas informações o enunciado nos pede para explicar o porquê de uma pessoa sentir frio no inverno e estar confortável no verão, em uma linguagem física.
Passo 2
Para resolver essa questão, nós vamos considerar que o Bart é um “objeto” pequeno em um meio muuuito grande.
O conforto térmico está ligado à perda de calor do corpo humano, e o que chamamos de frio está associado à perda excessiva de calor. Como a temperatura do ar é fixa, os diferentes níveis de conforto no verão e no inverno não podem ser atribuídos à transferência de calor por convecção do corpo. Nos dois casos (verão e inverno), o fluxo de calor por convecção é:
Substituindo os valores, temos,
Agora já sabemos como se comporta o fluxo de calor por convecção, mas e pela radiação?
Passo 3
No caso da radiação, o fluxo de calor vai ser diferente para o verão e para o inverno. Para o caso do verão, temos:
Substituindo os valores (lembra de passar a temperatura de para hein!),
E para o inverno, temos:
Com isso, vemos uma diferença significativa entre os fluxos de radiação do inverno e do verão, e a condição de resfriado é devido ao efeito das paredes mais frias na radiação.
Resposta
vemos uma diferença significativa entre os fluxos de radiação do inverno e do verão, e a condição de resfriado é devido ao efeito das paredes mais frias na radiação.