Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 21
Um aquecedor elétrico encontra-se no interior de um longo cilindro de diâmetro igual a . Quando água, a uma temperatura de e velocidade de , escoa perpendicularmente ao cilindro, a potência por unidade de comprimento necessária para manter a superfície do cilindro a uma temperatura uniforme de é de . Quando ar, também a , mas a uma velocidade de está escoando, a potência por unidade de comprimento necessária para manter a mesma temperatura superficial é de . Calcule e compare os coeficientes de transferência de calor por convecção para os escoamentos da água e do ar.
Passo 1
A questão nos fala que temos um cilindro longo de de diâmetro com um aquecedor elétrico incorporado com potência necessária para manter uma temperatura superficial especificada para os fluxos de água e ar, beleza? Ilustrando isso ficamos com o seguinte:
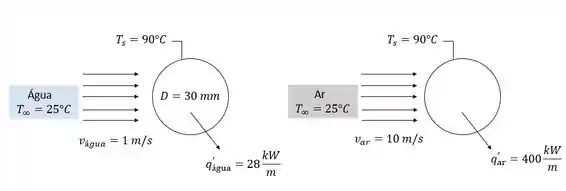
E nos é pedido para calcular e comparar os coeficientes de transferência de calor por convecção para os dois escoamentos.
Passo 2
Para resolver essa questão vamos assumir que o fluxo é transversal ao longo do cilindro, que é muito longo na direção normal do fluxo. Partindo disso, vamos ter que utilizar nossa famosa equação da taxa de convecção:
A partir dela, vamos isolar o coeficiente de transferência de calor por convecção e ficar com:
Agora só precisamos jogar os valores que temos tanto para água quanto para o ar na fórmula.
Passo 3
Substituindo os valores fornecidos pelo enunciado na fórmula do coeficiente de transferência de calor por convecção ficamos com, para água:
E para o ar,
Passo 4
Comparando os valores encontrados para o coeficiente de transferência de calor por convecção vemos que :
Repara que mesmo a velocidade do ar sendo 10 vezes maior que a da água . Outra informação que notamos é que esses valores para o coeficiente de convecção são típicos para transferência de calor por convecção forçada com líquidos e gases.