Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 12.Problemas - Ex. 97
O equipamento para aquecer uma pastilha durante um processo de fabricação de semicondutores é mostrado na figura. A pastilha é aquecida por uma fonte de feixe de íons (não mostrada) até uma temperatura uniforme e em estado estacionário. A grande câmara contém o gás de processo e as suas paredes estão a uma temperatura uniforme de . Uma área alvo de sobre a pastilha é focada por um radiômetro, cuja lente objetiva tem um diâmetro de e está localizada distante da pastilha. A linha de visão do radiômetro está a da normal da pastilha.
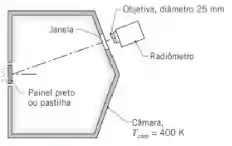
(a) Em um teste de pré-produção do equipamento, um painel preto é colocado no lugar da pastilha. Calcule a potência radiante recebida pelo radiômetro, sendo a temperatura do painel igual a
(b) A pastilha, que é opaca, difusa e cinza, com uma emissividade de , encontra-se agora posicionada no equipamento e o feixe de íons é ajustado de tal forma que a potência recebida pelo radiômetro é a mesma que foi encontrada na parte (a). Calcule a temperatura da pastilha para essa condição de aquecimento.
Passo 1
Olaaa, tudo bem?! Nessa questão nós temos uma pastilha aquecida por uma fonte de feixe de íons dentro de uma grande câmara de gás de processo com paredes a temperatura uniforme.
O radiômetro visualiza um alvo de na pastilha e possui um painel preto montado no lugar da bolacha em um teste de pré-produção do equipamento.
Com isso vamos encontrar a potência radiante recebida pelo radiômetro quando a temperatura do painel preto é e a temperatura da bolacha, , quando a fonte de feixe de íons é ajustada para que a energia radiante recebida pelo radiômetro é o mesmo da parte (a).
Passo 2
Para resolver essa questão vamos assumir:
(1) Condições de estado estacionário;
(2) A câmara representa um ambiente isotérmico grande;
(3) A bolacha é opaca, cinza-difusa;
(4) Área-alvo
A potência radiante que sai do alvo do painel preto e atinge o radiômetro é,
Onde e o ângulo sólido que o radiômetro subtende em relação ao alvo é,
Com encontramos,
Passo 3
Com a pastilha montada, a fonte do feixe de íons é ajustada até que o radiômetro receba a mesma potência radiante da parte (a) do painel preto. A potência que atinge o radiômetro é expressa em termos da radiosidade da pastilha,
Como , temos que:
Onde a radiosidade é,
E é igual à potência emissiva do corpo negro em . Utilizando as equações anteriores e substituindo os valores numéricos, encontramos,