Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 26

No esquema da figura, o nível da água é mantido constante. Determinar:

  1. O coeficiente de velocidade;
  2. O número de Reynolds teórico;
  3. O tempo que a água levará para subir 10   c m ao fechar o registro do bocal;
  4. A distância atingida pelo jato, pressurizando-se o tanque com ar comprimido, com P = 20   k P a ;
  5. A perda de carga no bocal, supondo a perda na válvula desprezível.

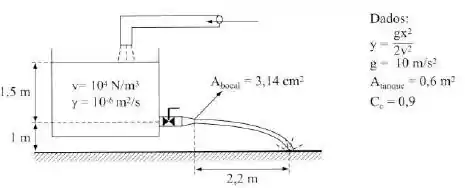
Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Para a velocidade teórica, vamos aplicar Bernoulli entre 1 - 2 :

P 1 γ + v 1 2 2 g + z 1 = P 2 γ + v 2 2 2 g + z 2

1,5 = v 2 2 20

v 2 t = 5,47   m / s

Para calcular a velocidade real, vamos observar a trajetória que a água faz a partir da saída do bocal, cuja expressão é dada no problema por:

y = g x 2 2 v 2

1 = 10 2,2 2 2 v 2

v 2 R = 4,91   m / s

O coeficiente de velocidade será:

C v = 4,91 5,47

C v = 0,9

Passo 2

Considerando o diâmetro de escoamento na saída a partir da área dada do bocal, temos:

A = π D 2 4

D = 0,02   m

Conhecido o diâmetro teórico, Reynolds é dado por:

R e = v T D v

R e = 5,47 0,02 10 - 6

R e = 1,1 ⋅ 10 5

Passo 3

Como temos as constantes de velocidade e de contração, podemos calcular o fluxo real de saída:

Q = C v C c Q T

Q = 0,9 0,9 3,14 ⋅ 10 - 4 4,91

Q = 1,23 ⋅ 10 - 3   m 3 / s

O fluxo de subida é dado por:

Q = v s u b i d a A t

v s u b i d a = 1,23 ⋅ 10 - 3 0,6

Portanto:

0,1 ∆ t = 1,23 ⋅ 10 - 3 0,6

∆ t = 49   s

Passo 4

Caso o tanque fosse pressurizado, o sistema mudaria. Vamos calcular a nova velocidade teórica de saída por Bernoulli:

P 1 γ + v 1 2 2 g + z 1 = P 2 γ + v 2 2 2 g + z 2

20 ⋅ 10 3 10 4 + 1,5 = v 2 2 2 g

v 2 T = 8,36   m / s

A velocidade real será:

C v = v R v T

0,9 = v R 8,36

v R = 7,53   m / s

Assim podemos calcular a nova distância atingida:

y = g x 2 2 v 2

1 = 10 x 2 2 7,53 2

x = 3,37   m

Passo 5

Podemos verificar que a perda de carga no bocal se dá em função da diferença entre a velocidade real e teórica do escoamento. Utilizaremos o coeficiente de velocidade calculado na alternativa a para obter a velocidade real do escoamento:

v T = 2 g h

v T = 2 9,81 1,5

v T = 5,477   m / s

Utilizaremos o coeficiente de velocidade C v = 0,9 :

v R = 0,9 ⋅ 5,477

v R = 4,929   m / s

Utilizando as duas velocidades, podemos encontrar a perda de carga no bocal delgado:

h b o c a l = v T 2 - v R 2 2 g

h b o c a l = 5,477 2 - 4,929 2 2 ⋅ 10

h b o c a l = 0,285   m

Resposta

a )   C v = 0,9

b )   R e = 1,1 ⋅ 10 5

c )   ∆ t = 49   s

d ) x = 3,37   m  

e ) h b o c a l = 0,285   m  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Qual é o princípio operacional dos medidores de vazão de área variável (rotâmetros)? Como eles se comparam aos outros tipos de medidor de vazão com relação ao custo, perda de carga e confiabilidade?
Quais são as principais considerações ao selecionar um medidor de vazão para medir a vazão de um fluido?
Qual a diferença entre os princípios operacionais dos anemômetros térmicos e laser Doppler?
Explique como a vazão é medida com medidores de vazão do tipo por obstrução. Compare os medidores de orifício, de bocais de escoamento e os medidores de Venturi com relação ao custo, tamanho, perda de
Explique como a vazão é medida com um tubo estática de Pitot e discuta suas vantagens e desvantagens com relação ao custo, queda de pressão, confiabilidade e exatidão.