Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Brunetti - Mecânica dos Fluidos - Ed: 2º - Capítulo Exercícios Selecionados.- - Ex. 23

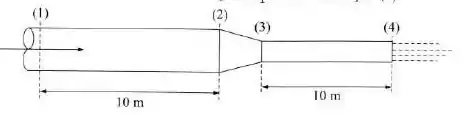
No trecho 1 - ( 2 ) do conduto da figura, o escoamento do fluido ( γ = 8000   N / m 3 ) é laminar, a vazão é 10   L / s , o diâmetro é 8   c m e o R e = 1000 . No trecho 3 - 4 o diâmetro é 6   c m . O coeficiente da perda de carga da singularidade 2 - 3 é 1 , referente à maior velocidade. Qual a pressão na seção 1 ?

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Como sabemos, existem dois tipos de perdas no sistema: por singularidade e por carga distribuída.

Podemos inferir que a nossa equação da energia será:

H 1 = H 4 + H s + H f 1 + H f 2

Vamos calcular cada termo separadamente para ficar mais organizado:

H 1 = P 1 γ + v 1 2 2 g

A velocidade no ponto 1 é calculada pela relação de fluxo volumétrico e área:

v 1 = Q A 1

v 1 = 4 Q π D 1 2

Substituindo as variáveis, temos que:

v 1 = 4 10 ⋅ 10 - 3 π 8 ⋅ 10 - 2 2

v 1 = 1,99   m / s

Analogamente, a velocidade no ponto 4 será:

v 4 = Q A 4

v 4 = 4 Q π D 4 2

Substituindo as variáveis, temos que:

v 4 = 4 10 ⋅ 10 - 3   π 6 ⋅ 10 - 2 2

v 4 = 3,54   m / s

Passo 2

Agora façamos o cálculo das parcelas de perdas:

H s = k s v 4 2 2 g

H s = 1 3,54 2 2 0

H s = 0,63   m

Para escoamentos laminares, temos que:

f = 64 R e

f = 0,064

Assim, para a perda por carga distribuída no primeiro trecho:

H f 1 = f L D 1 ⋅ v 1 2 2 g

H f 1 = 0,064 10 8 ⋅ 10 - 2 ⋅ 1,99 2 2 0

H f 1 = 1,58   m

Analogamente, temos que:

H f 2 = f L D 2 ⋅ v 2 2 2 g

H f 2 = 0,064 10 6 ⋅ 10 - 2 ⋅ 3,54 2 2 0

H f 2 = 6,68   m

Passo 3

Portanto, teremos que:

P 1 8000 + 1,99 2 20 = 3,54 2 20 + 0,63 + 1,58 + 6,68

P 1 = 65,12   k P a

Resposta

P 1 = 65,12   k P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em uma posição axial específica, os perfis de velocidades e de temperaturas para o escoamento laminar em um canal entre placas paralelas têm as formas: u y = 0,751 - y y 0 2 T y = 5,0 + 95,66 y y 0 2
Um resfriador de óleo de motor tem um feixe de 25 tubos lisos, cada um com comprimento L = 2,5 m e diâmetro D = 10 mm. Se óleo a 300 K e a uma vazão mássica total de 24 k g s escoa em condições plenam
Para o escoamento laminar plenamente desenvolvido através de um canal entre placas paralelas, o componente na direção x da equação do momento tem a forma: μ d 2 u d y 2 = d p d x = c o n s t a n t e O
Considere água pressurizada, óleo de motor (não usado) e NaK ( 22 % / 78 % ) escoando em um tubo com 20 mm de diâmetro. Determine a velocidade média, o comprimento de entrada fluidodinâmico e o compri
Glicerina a 40 ° C com ρ = 1,252k g / m 3 e μ = 0,27k g / m . s escoa através de um tubo suave horizontal com 5c m de diâmetro e velocidade média de 3,5m / s . Determine a queda de pressão por 10m do