Um esquema que permite estender as condições de operação das lâminas de turbina a gás até temperaturas mais elevadas envolve a aplicação de um revestimento cerâmico nas superfícies das lâminas que, por sua vez, são fabricadas com uma superliga, o inconel. Para avaliar a confiabilidade de tais revestimentos, foi desenvolvido um equipamento para testar amostras sob condições de laboratório. A amostra é colocada na parte inferior de uma grande câmara de vácuo, cujas paredes são resfriadas criogenicamente e que é equipada com um detector de radiação na sua superfície superior. O detector tem uma área superficial , está localizado a uma distância da amostra e vê a radiação que se origina em uma porção da superfície cerâmica com área . Um aquecedor elétrico fixado à parte inferior da amostra dissipa um fluxo térmico uniforme , que é transferido para cima através da amostra. A parte inferior do aquecedor, bem como as laterais da amostra, estão termicamente isoladas.
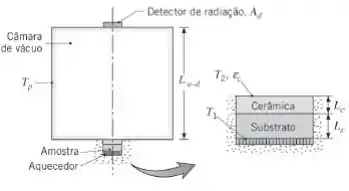
Considere condições nas quais um revestimento cerâmico com espessura e condutividade térmica foi borrifado sobre um substrato metálico que tem espessura e condutividade térmica A superfície opaca do material cerâmico pode ser aproximada por uma superfície cinza e difusa, com uma emissividade hemisférica total de .
(a) Considere condições de regime estacionário nas quais a superfície inferior do substrato é mantida a , enquanto as paredes da câmara (incluindo a superfície do detector de radiação) são mantidas a . Admitindo resistência térmica de contato desprezível na interface cerâmica-substrato, determine a temperatura na superfície superior do material cerâmico e o fluxo térmico .
(b) Para as condições dadas, qual é a taxa na qual a radiação emitida pela cerâmica é interceptada pelo detector?
(c) Após um grande número de experimentos, várias rachaduras apareceram na interface cerâmica-substrato, criando uma resistência térmica do contato nessa interface. Se e forem mantidos nas condições associadas à parte (a), o valor de irá aumentar, diminuir ou permanecer o mesmo? Analogamente, o valor de irá aumentar, diminuir ou permanecer o mesmo? Em cada caso, justifique sua resposta.
Passo 1
Maaaanx, que enunciado ENORME, ne? Mas calma que eu resumi pra você
Além, também, das temperaturas da parede da câmara de vácuo e superfície inferior do substrato, área de recepção do detector de radiação, distância do detector da amostra e área de superfície da amostra visualizada pelo detector. Onde o circuito térmico é:
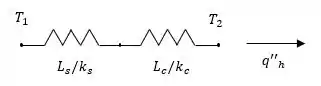
Com isso, vamos encontrar a temperatura da superfície superior da cerâmica e fluxo de calor, a taxa na qual a radiação emitida pela cerâmica é interceptada pelo detector e o efeito de uma resistência de contato interfacial (cerâmica / substrato) nas temperaturas da superfície superior e inferior da amostra. Vamos lá!
Passo 2
Para resolver essa questão vamos assumir:
(1) Condução unidimensional em estado estacionário na amostra;
(2) Propriedades constantes;
(3) A câmara forma um invólucro de corpo preto em ;
(4) A superfície cerâmica é difusa/cinza;
(5) A resistência de contato da interface é desprezível para a peça (uma).
A partir de um balanço energético na superfície cerâmica exposta temos,
Ou,
Substituindo os valores,
Resolvendo essa equação, encontramos:
E,
Passo 3
Como a superfície da cerâmica é difusa, a intensidade total da radiação emitida em todas as direções é,
Portanto, a taxa na qual a radiação emitida é interceptada pelo detector é,
Com o desenvolvimento de uma resistência de contato térmico interfacial e valores fixos de :
- permanece o mesmo (seu valor é determinado pelo requisito de que ) enquanto,
- aumenta (seu valor é determinado pelo requisito de que onde , se e são fixos, deve aumentar com o aumento de ).
Fim! 😊
Resposta
- permanece o mesmo e aumenta.