No Exemplo 10.1 analisamos condições nas quais uma ebulição vigorosa ocorre em uma panela de água e nós determinamos a potência elétrica (taxa de transferência de calor) requerida para manter uma temperatura especificada na base da panela. Entretanto, a potência elétrica é, na verdade, a variável de controle (independente), que tem como consequência de seu valor a temperatura da panela.

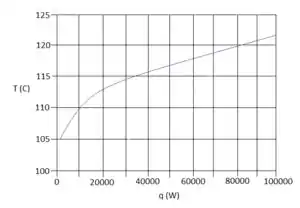
1. Para a ebulição nucleada na panela de cobre do Exemplo 10.1, calcule e represente graficamente a temperatura da panela como uma função da taxa de transferência de calor para 1 ≤ q ≤ 100 kW.
2. Se a temperatura inicial da água fosse igual à temperatura da sala, obviamente, ela teria que ser aquecida por um período de tempo até que entre em ebulição. Considere condições logo após o início do aquecimento e que a água esteja a 20°C. Estime a temperatura da base da panela para uma taxa de transferência de calor de 8 kW.

Começando pela letra a, precisamos calcular a temperatura e representar graficamente, belezinha?

Então vamos começar com os cálculos:

Vamos achar esse :

Vamos achar a área:

E considerando ; e , teremos o seguinte:

Então vamos ficar com um temperatura de:

Agora partiu fazer o gráfico com :

Agora na letra b, vamos estimar a temperatura da base da panela, considerando uma taxa de transferência de calor de .

Vamos usar essa relação aqui, olha só:

Vamos achar o , ok?

Sendo:

E substituindo a equação de na nossa equação ali de cima:

Temos que deixar em função da temperatura que a gente não tem ainda, ok?

Então vamos colocar isso na equação lá de cima!