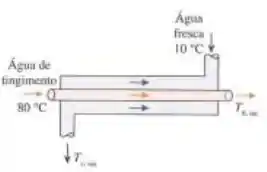
Em uma fábrica têxtil, águas residuais de tingimento a 80 °C devem ser utilizadas para preaquecimento de água fresca a 10 °C com a mesma vazão em um trocador de calor de tubo duplo em contracorrente. A superfície de transferência de calor do trocador de calor da água é , e o coeficiente global de transferência de calor é . Considerando que a taxa de transferência de calor no trocador de calor é 35 kW, determine a temperatura de saída e a vazão mássica de cada fluido.

Ao desenvolvermos esta questão vamos perceber um probleminha gerado pela falta de resultados, mas que é possível de resolver com auxílio de programas para resolução de sistemas de equação.

Mas não vamos nos preocupar ainda com isto, vamos começar a desenvolver a questão em si!

Vamos começar desenvolvendo as nossas relações. Para o cálculo da taxa de transferência de calor, podemos utilizar a seguinte relação:

Percebam que a questão já nos deu a taxa de transferência de calor, o coeficiente global de troca de calor e a área de superfície. Só nos resta a diferença de temperatura logarítmica. Logo, calculando-o, temos:

Portanto, a nossa relação é:

E por enquanto paramos por aqui. Não conseguimos determinar nenhuma das temperaturas ainda!