Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 9.Problemas - Ex. 39

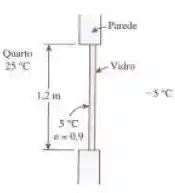
Considere uma janela de vidro de 1,2 m de altura e 2 m de largura com espessura de 6 mm, condutividade térmica k = 0,78   W / m ⋅ K e emissividade ε = 0,9 . A sala e as paredes voltadas para a janela são mantidas a 25 °C, e a temperatura média da superfície interna da janela é 5 °C, determine (a) o coeficiente de transferência de calor por convecção na superfície interna da janela, (b) a taxa total de transferência de calor através da janela e (c) o coeficiente combinado de transferência de calor por convecção natural e radiação na superfície externa da janela. É razoável desprezar a resistência térmica do vidro, neste caso?

Passo 1

Vamos lá! É sempre importante começarmos pela colocação das nossas hipóteses do problema! Nesta questão temos uma operação de convecção natural, em regime permanente, o ar é considerado um gás ideal e as suas propriedades são constantes!

Começaremos pela determinação do coeficiente h . Para isto, vamos utilizar a temperatura de filme T f = 25 + 5 / 2 = 15   ° C .

Começando pelo número de Rayleigh, temos:

R a L = g β T s - T ∞ L c 3 ν 2 P r = g T s - T ∞ L c 3 T f ⋅ ν 2 P r

R a L = 9,81 ⋅ 25 - 5 ⋅ 1,2 3 15 + 273 ⋅ 1,470 ⋅ 10 - 5 2 ⋅ 0,7323 = 3,989 ⋅ 10 9

Agora, o número de Nusselt é dado por:

N u = h L c k = 0,825 + 0,387 ⋅ R a 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

Portanto, o coeficiente h é:

h = k L c ⋅ 0,825 + 0,387 ⋅ R a 1 / 6 1 + 0,492 P r 9 / 16 8 / 27 2

h = 0,02476 1,2 ⋅ 0,825 + 0,387 ⋅ 3,989 ⋅ 10 9 1 / 6 1 + 0,492 0,7323 9 / 16 8 / 27 2

h = 3,915   W / m 2 ⋅ K

Finalizando a letra a).

Passo 2

Agora, vamos calcular a taxa total de transferência de calor. Para isto, vamos considerar ambos os efeitos da convecção e da radiação. Desta forma, temos:

Q ˙ = Q ˙ c o n v + Q ˙ r a d

Q ˙ = h A s T s - T ∞ + ε σ A s T s 4 - T c i r 4

Q ˙ = 3,915 ⋅ 2,4 ⋅ 25 - 5 + 0 , 9 ⋅ 5,67 ⋅ 10 - 8 ⋅ 2,4 ⋅ 298 4 - 2 78 4

Q ˙ = 422,2   W

Passo 3

Para podermos encontrar o coeficiente combinado, precisamos determinar inicialmente a temperatura externa da janela. Para isto, basta aplicarmos a lei de Fourier. Logo,

Q ˙ = k A L Δ T = k A Δ T L T s - T e x t

T e x t = T s - Q ˙ L k A = 5 - 422,2 ⋅ 0,006 0,78 ⋅ 2,4

T e x t = 3,65   ° C

Agora, podemos aplicar esta temperatura na lei da convecção para descobrirmos o coeficiente combinado. Portanto,

Q ˙ = h c o m b A T e x t - T ∞

h c o m b = Q ˙ A T e x t - T ∞ = 422,2 2,4 ⋅ 3,65 - - 5

h c o m b = 20,3   W / m 2 ⋅ K

Passo 4

Em relação a resistência do vidro, se ela é desprezível ou não, basta compararmos as quedas de temperatura.

Podemos fazer isto pois a resistência térmica é diretamente proporcional a variação de temperatura para cada elemento.

Portanto, a resistência térmica do vidro em comparação a todo o sistema corresponde a:

R v i d r o R t o t a l = Δ T v i d r o Δ T t o t a l = 5 - 3,65 25 - - 5 = 0,045 = 4,5   %

Como este valor é baixo, menor que 5%, podemos desconsiderar a resistência térmica do vidro sim.

Resposta

  1. O coeficiente de transferência de calor é:

    2. h = 3,915   W / m 2 ⋅ K

  2. A taxa total de transferência de calor é:

    3. Q ˙ = 422,2   W

  3. O coeficiente combinado de transferência de calor é:

h c o m b = 20,3   W / m 2 ⋅ K

Podemos desconsiderar sim o efeito da resistência térmica do vidro.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A janela traseira vertical de um automóvel tem uma espessura L=8m m e uma altura H=0,5m . O vidro contém fios aquecedores formando uma malha fina que podem induzir um aquecimento volumétrico praticame
Seja o transformador do Problema 8.103, cuja superfície lateral está sendo mantida a 47 ° C por uma linha de refrigerante por convecção forçada que remove 1000W . Deseja-se estudar o resfriamento do t
No conceito de coleta centralizada em uma planta de potência solar, muitos espelhos no nível do solo são usados para direcionar um fluxo solar concentrado q s ' ' para o receptor, que se encontra posi
Um experimento envolve o aquecimento de uma esfera bem pequena, que se encontra suspensa por um fio fino em ar, com um raio de laser para induzir a maior temperatura possível na esfera. Após verificar
Um cilindro horizontal, com 25m m de diâmetro, é mantido com uma temperatura superficial uniforme de 35 ° C . Um fluido com uma velocidade de 0,05m / s e uma temperatura de 20 ° C escoa, em escoamento