Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 59
A figura ilustra esquematicamente um difusor cônico, que é projetado para aumentar a pressão e diminuir a energia cinética. Vamos considerar que o ângulo α seja pequeno ( de modo que e , em que ri é o raio de entrada do difusor, é o raio na saída e é o comprimento do difusor. O escoamento em um difusor é complexo, mas aqui vamos considerar que cada camada do escoamento do fluido no difusor é laminar, como em um tubo cilíndrico com seção transversal de área constante. Baseado em um raciocínio similar aquele apresentado na Seção 8.3, a diferença de pressão entre as extremidades de um tubo cilíndrico é
em que é a localização no difusor, é a viscosidade dinâmica do fluido e é a vazão. A equação acima é aplicável para escoamentos em um difusor considerando que a força inercial e efeitos de saída são desprezíveis. Deduza uma expressão para a resistência hidráulica, , do difusor.
Passo 1
Neste problema é apresentado um escoamento laminar ao longo de um difusor cônico e solicitada a expressão da resistência hidráulica ().
Sabendo que:
E que o enunciado forneceu a diferença de pressão entre as extremidades do tubo conforme expressão:
Então, o poderá ser calculado como:
Passo 2
O cálculo de exigirá a obtenção da variável como função de , pois a integral a ser desenvolvida é com relação ao parâmetro .
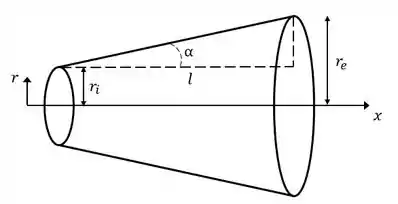
Considerando a Figura acima e aplicando trigonometria, sabendo que o enunciado admitiu que , então pode-se escrever que:
De forma que pode ser escrito como sendo função de :
Passo 3
Então conhecendo a expressão de e como função de , é possível desenvolver a seguinte expressão:
Usando o método de substituição para resolver a integral e fazendo:
De forma que:
Considerando as variáveis de substituição, é escrito como:
Realizando a integração:
Logo, a resistência hidráulica para este problema tem a seguinte expressão: