Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 8.Problemas - Ex. 68

Querosene é bombeado através de um tubo liso com diâmetro interno D = 30 mm, na proximidade do número de Reynolds crítico. O escoamento é instável e flutua entre os estados laminar e turbulento, fazendo com que o gradiente de pressão varie intermitentemente de -4,5 kPa/m a -11 kPa/m, aproximadamente. Que gradiente de pressão corresponde ao escoamento laminar e ao escoamento turbulento? Para cada escoamento, calcule a tensão de cisalhamento na parede do tubo e trace as distribuições de tensão de cisalhamento.

Passo 1

Neste problema o escoamento está em uma faixa de instabilidade, tendo comportamento laminar e turbulento, o que implica em variação de gradiente de pressão.

Assim dois gradientes de pressão foram medidos:

∂ p 1 ∂ x = - 4,5   k P a / m  

∂ p 2 ∂ x = - 11   k P a / m  

Com tais informações, o objetivo é definir qual gradiente de pressão corresponde ao escoamento laminar e turbulento.

Para isso deverá ser calculado a tensão de cisalhamento do tubo para os dois gradientes de pressão, pois sabe-se que em escoamentos turbulentos há a presença de tensões adicionais.

Considerando escoamento completamente desenvolvido, a tensão de cisalhamento é dada por:

τ r x = r 2 ∂ p ∂ x  

Passo 2

Usando a expressão da tensão de cisalhamento e aplicando-a para os dois gradientes de pressão.

- τ r x 1

τ r x 1 = r 2 ∂ p 1 ∂ x  

τ r x 1 = D 2 2 ∂ p 1 ∂ x  

τ r x 1 = D 4 ∂ p 1 ∂ x  

Usando os valores numéricos de D = 30   m m e ∂ p 1 / ∂ x = - 4,5   k P a :

τ r x 1 = 30 × 10 - 3 4 ( - 4,5 × 10 3 )  

τ r x 1 = - 33,75   P a  

- τ r x 2

τ r x 2 = D 4 ∂ p 2 ∂ x  

Usando os valores numéricos de D = 30   m m e ∂ p 2 / ∂ x = - 11   k P a :

τ r x 2 = 30 × 10 - 3 4 ( - 11 × 10 3 )  

τ r x 2 = - 82,50   P a  

Note que o sinal negativo do termo τ r x 1 e τ r x 2 indica o sentido de atuação da tensão de cisalhamento, o qual é contrário ao escoamento.

Passo 3

Avaliando o resultados calculados de tensão de cisalhamento, nota-se que:

τ r x 2 = 82,50 > τ r x 1 = 33,75    

Com tal informação pode-se afirmar que: ∂ p 1 / ∂ x corresponde ao escoamento laminar e ∂ p 2 / ∂ x ao escoamento turbulento.

Passo 4

Segundo a teoria, para escoamentos completamente desenvolvidos, laminares ou turbulentos, a tensão de cisalhamento varia linearmente através do tubo, desde zero, na linha de centro, até o valor máximo na parede do tubo.

Graficamente, para os casos avaliados, o comportamento de tensão de cisalhamento ao longo do raio do tubo até sua parede é visto por:

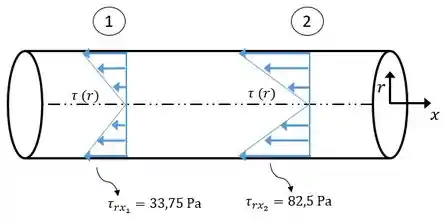
Resposta

- gradiente de pressão ∂ p 1 / ∂ x : regime laminar;

- gradiente de pressão ∂ p 2 / ∂ x : regime turbulento;

- tensão de cisalhamento na parede (para ∂ p 1 / ∂ x )

τ r x 1 = - 33,75   P a  

- tensão de cisalhamento na parede (para ∂ p 2 / ∂ x )

τ r x 2 = - 82,50   P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O perfil de velocidade para escoamento completamente desenvolvido de óleo castor a 20 °C entre placas paralelas em movimento, é dado pela Eq. 8.8. Considere U = 1,5m / s e a = 5m m . Determine o gradi
O perfil de velocidade para escoamento completamente desenvolvido de tetracloreto de carbono a 15 °C entre placas paralelas (espaçamento a = 1,25m m ), com a placa superior em movimento, é dado pela E
Glicerina a 15 °C escoa entre placas paralelas com espaçamento b = 2,5m m entre elas. A placa superior move com velocidade U = 0,6m / s no sentido positivo de x . O gradiente de pressão é ∂ p / ∂ x =
Um inventor propõe fabricar um “cronômetro viscoso” colocando um cilindro pesado dentro de outro cilindro ligeiramente maior contendo um líquido viscoso, formando assim uma película anular delgada ent
Uma película de tinta molhada de espessura uniforme, δ , está pintada sobre uma parede vertical. A tinta molhada pode ser aproximada como um fluido de Bingham com tensão de escoamento τ y e massa espe