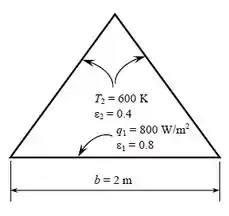
Um forno é moldado como um logo duto triangular equilátero em que a largura de cada lado é 2 m. Calor é fornecido a partir da superfície da base, cuja emissividade é de , a uma taxa de 800 W/m², enquanto as superfícies lateriais com emissivdades 0,4 são mantidas a 600K. Desprezando os efeitos das extremidades, determine a temperatura da superfície da base. Você pode tratar essa geometria como um recinto de duas superfícies?

Essa questão é aplicação direta de uma fórmula que está em formulários. Mas devemos considerar que a geometria pode ser tratada como duas superfícies enclausuradas desde que as duas superfícies tenham propriedades indênticas. Vamos chamar a superfícies da base como 1 e as outras superfícies como sendo 2. Portanto o fator de forma F12 = 1 e a temperatura da superfície da base pode ser calculada a fórmula que te falei lá no início, se liga!

Onde q12 = 800 W

T2 = 600 K

Substituindo esses valores, encontraremos o valor de T1 = 630 K

E note que A1 = 1 m² e A2 = 2 m²