Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 1.Problemas - Ex. 57
Um forno para o processamento de materiais semicondutores é formado por uma câmara de carbeto de silício que tem uma zona quente na seção superior e uma zona fria na seção inferior. Com o elevador na posição inferior, um braço robô insere a pastilha de silício nos pinos de apoio. Em uma operação de produção, a pastilha é rapidamente deslocada para a zona quente para cumprir o histórico temperatura-tempo especificado para o processo. Nesta posição, as superfícies superior e inferior da pastilha trocam radiação com as zonas quente e fria, respectivamente, da câmara. As temperaturas das zonas são Tq = 1500 K e Tf = 330 K, e as emissividade e espessura da pastilha são ε = 0,65 e d = 0,78 mm, respectivamente. Com o gás no ambiente a T∞ = 700 K, os coeficientes de transferência de calor por convecção nas superfícies superior e inferior da pastilha são 8 e 4 W/(m2 · K), respectivamente. A pastilha de silício tem uma densidade de 2700 kg/m3 e um calor específico de 875 J/(kg · K).
(a) Para uma condição inicial que corresponde a uma temperatura da pastilha de Tp,i = 300 K e a posição da pastilha como mostrado no esquema, determine a taxa de variação temporal da temperatura da pastilha correspondente (dTp/dt)i.
(b) Determine a temperatura no estado estacionário que a pastilha atinge se ela se mantiver nesta posição. O quanto a transferência de calor por convecção é significativa nesta situação? Esboce como você espera que a temperatura da pastilha varie como uma função da posição vertical do elevador.
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Temos uma pastilha de silício em um forno com duas zonas diferentes: uma quente, na parte superior, com uma temperatura de nas vizinhanças, e uma fria, na parte inferior, com uma temperatura de . Além disso, há gás dentro no forno à temperatura de .
A gente vai olhar agora um momento onde essa pastilha troca calor tanta com a parte quente quanto com a parte fria do forno, com os mecanismos de transferência de calor demonstrados no esquema ilustrativo abaixo:
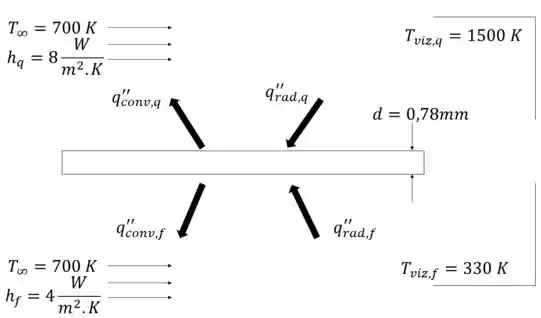
Olhando para essa imagem, podemos fazer o seguinte balanço integral de energia na pastilha inteira:
Sendo:
- a taxa de acúmulo de energia térmica por unidade de área;
- é o fluxo de calor radiante que entra na pastilha a partir do lado quente;
- é o fluxo de calor radiante que entra na pastilha a partir do lado frio;
- é o fluxo de calor convectivo que entra na pastilha a partir do lado quente;
- é o fluxo de calor convectivo que entra na pastilha a partir do lado frio.
Se destrincharmos cada um dos tipos de fluxo, podemos calculá-los a partir das equações:
Sendo a temperatura da superfície da pastilha, a temperatura do gás, a temperatura das vizinhanças (que é diferente para os lados quente e frio), o coeficiente de transferência de calor (que é diferente para os lados quente e frio), a emissividade da pastilha e a constante de Stefan–Boltzmann.
Sendo assim, no item (a) devemos calcular para uma temperatura inicial de .
No item (b), devemos calcular a temperatura da superfície no estado estacionário () para as outras condições mantidas iguais. Além disso, nesse mesmo item, devemos também fazer um esboço de um gráfico da variação da temperatura da pastilha com relação a posição vertical.
Pois é, a gente já começou falando muito né? Mas antes da gente ir pro próximo passo, eu quero que você guarde algumas propriedades que vamos utilizar:
Passo 2
Para resolver o item (a), vamos reorganizar o balanço realizado no Passo 1:
Substituindo os valores por termo:
Vamos substituir a equação inteira:
Passo 3
Vamos resolver agora a primeira parte do item (b).
Considerando o estado estacionário (), nosso balanço de energia fica assim:
Devemos deixar essa equação toda em função de .
Primeiro, vamos deixar então os nossos fluxos convectivos em função da temperatura da superfície :
Agora, vamos deixar então os nossos fluxos radiantes em função da temperatura da superfície :
Substituindo tudo isso no balanço:
Reorganizando a equação para explicitar :
Para encontrar o valor de basta resolver a equação acima. Nesta resolução, foi utilizado o método de busca direta em uma calculadora, mas você pode se sentir livre para resolver da maneira que desejar. Sendo assim:
Vamos analisar esse mesmo resultado sem a transferência de calor por convecção:
Resolvendo a equação:
Vamos calcular o erro relativo entre esses dois valores:
Como temos um erro menor que 1%, fica claro que a transferência de calor por radiação controla o processo.
Passo 4
Pra fechar a questão, vamo responder agora a última parte da letra (b).
O esquema do gráfico de elevação por temperatura pode ser feito da seguinte forma:
Perceba que, quando mais próximo da zona fria, mais a temperatura tende a entrar em equilíbrio com suas vizinhanças e ficar em . Da mesma maneira, quanto mais o elevador sobe, mais a temperatura tende a assumir o valor de .
UFA! Demorou um pouco, mas a gente matou a questão juntos! :)
Resposta
(a) O valor da taxa de variação temporal da temperatura da pastilha é
(b) O valor da temperatura da superfície no estado estacionário é