Um reator esférico de aço inoxidável (AISI 302) é usado para armazenar um meio reacional que fornece um fluxo de calor uniforme para a sua superfície interna. O reator é subitamente submerso em um banho líquido a uma temperatura T∞
(a) Considerando que o gradiente de temperatura na parede do reator seja desprezível e um fluxo de calor constante e igual a q’’i, desenvolva uma equação para a variação da temperatura da parede em função do tempo durante o processo transiente. Qual é a taxa inicial de variação da temperatura na parede se q’’i = 105 W/m2?
(b) Qual a temperatura da parede em condições de regime estacionário?
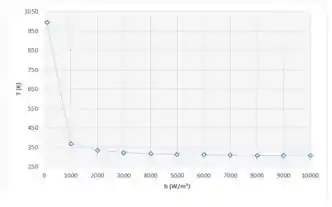
(c) O coeficiente de transferência de calor por convecção depende da velocidade do escoamento do fluido externo ao reator e do fato da temperatura da parede ser ou não elevada o suficiente para induzir a ebulição do líquido. Calcule e represente graficamente a temperatura da parede em regime estacionário em função do valor de h para a faixa 100 ≤ h ≤ 10.000 W/(m2 · K). Existe algum valor de h abaixo do qual a operação seria inaceitável?
Passo 1
Vamos analisar a questão juntos pra entendermos o que você deve fazer para revolvê-la.
Temos um reator esférico que gera um fluxo de calor e é submetido a convecção em um banho líquido com uma temperatura maior que a temperatura da superfície do reator, de acordo com o esquema representativo da imagem abaixo:
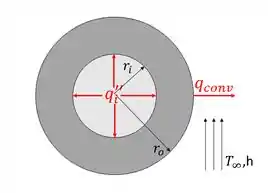
Pra resolver o item (a), devemos fazer um balanço de energia integral para o reator e calcular a taxa inicial de variação da temperatura da parede.
No item (b), devemos calcular a temperatura da superfície no estado estacionário para as outras condições mantidas iguais.
Por fim, no item (c), vamo colocar a temperatura da parede em função do coeficiente de convecção , variar esse valor de 100 a 10.000 e traçar um gráfico com os valores obtidos.
Pois é, a gente já começou falando muito né? Mas antes da gente ir pro próximo passo, eu quero que você guarde algumas propriedades que vamos utilizar:
Passo 2
Primeiro, a gente vai resolver a letra (a).
A partir da imagem esquemática do Passo 1, vamos fazer um balanço de energia na parede da esfera:
Considerando que, segundo o enunciado da questão, não há transferência de calor por condução na parede (pois o gradiente de temperatura na parede do reator seja desprezível), nosso balanço fica assim:
Sendo:
- , o volume da parede esférica;
- , a área da superfície interna da esfera;
- , a área da superfície externa da esfera;
Vamos reorganizar o balanço e explicitar :
Substituindo os valores das propriedades no balanço:
Passo 3
Vamos resolver o item (b).
Considerando o estado estacionário (), nosso balanço de energia fica assim:
Reorganizando a equação e substituindo os valores:
Passo 4
Pra fechar a questão, vamo responder a letra (c).
Vamo colocar agora a temperatura da superfície em função do coeficiente de convecção :
Vamos agora traçar um gráfico no Excel, variando de 100 a 10.000 :

Pronto, matamos a questão juntos! :)
Resposta
(a) O valor da taxa de variação temporal da temperatura do reator é
(b) O valor da temperatura da superfície no estado estacionário é
(c)