Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 124
Uma fresta estreita entre duas placas circulares está inicialmente preenchida com líquido incompressível. Em , a placa superior, inicialmente distate da placa inferior, começa a mover-se para baixo, de encontro a placa inferior, com velocidade constante, , provocando a expulsão do líquido através da fresta. Desprezando efeitos viscosos e considerando escoamento uniforme na direção radial, desenvolva uma expressão para o campo de velocidade entre as placas paralelas. Sugestão: Aplique a equação da conservação de massa a um volume de controle com superfície externa localizada no raio . Note que o escoamento não é permanente, embora a velocidade da placa superior seja constante. Para e , encontre a velocidade no raio de saída em e . Trace o gráfico da velocidade de saída em função do tempo, e explique a tendência.
Passo 1
Tá legal! Vamos começar esse exercício ilustrando o problema e desenhando o volume de controle conforme pedido no enunciado:
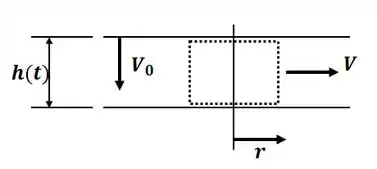
Vamos começar esse exercício aplicando o princípio da continuidade para o sistema, nesse caso, teremos:
Então, nesse caso, aplicando para o volume de controle desenhado, temos:
Nesse caso, sabemos que o volume pode ser escrito como:
E a área da seção será:
Então a equação de cima se torna:
Passo 2
No entanto, a variação altura pode ser escrita em função da velocidade de aproximação do disco superior, então, temos:
Dessa forma, a equação se torna:
Só que, como é constante, então, podemos escrever a altura como:
Então, substituindo essa expressão na equação anterior, temos:
Passo 3
Beleza, agora vamos ecnontrar a velocidade no raio de saída em e , então, temos:
Passo 4
E o gráfico da velocidade de saída em função do tempo será:
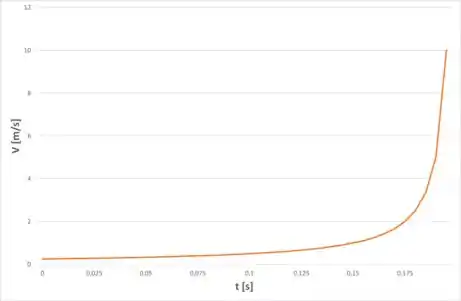
A velocidade vai aumentando com o tempo porque o espaço que o fluido tem para escoar vai ficando cada vez menor com a aproximação do disco superior, que vai pressionando o fluido para fora.