Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Fox - Mecânica dos Fluidos- Ed: 8º - Capítulo 4.Problemas - Ex. 115

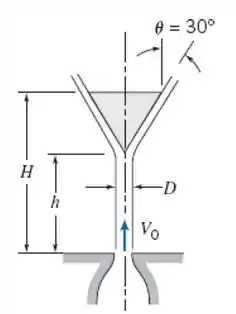
A água de um jato de diâmetro D é usada para suportar o objeto cônico mostrado. Deduza uma expressão para a massa combinada do cone e da água, M , que pode ser suportada pelo jato, em termos de parâmetros associados a um volume de controle adequadamente escolhido. Use a expressão obtida para calcular M quando V 0 = 10   m / s , H = 1   m , h = 0,8   m , D = 50   m m e θ = 30 ° . Estime a massa de água no volume de controle.

Passo 1

Tá legal! Vamos começar esse exercício desenhando o volume de controle a ser utilizado:

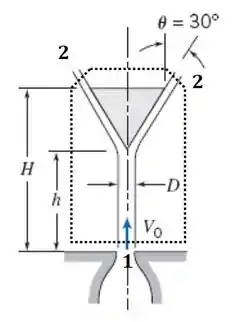
Vamos começar esse exercício aplicando o princípio da continuidade para o sistema, onde a vazão que entra em 1 deve sair em 2, então, temos:

m ˙ = ρ V 1 A 1 = ρ V 2 A 2 → V 1 A 1 = V 2 A 2

Agora vamos aplicar a equação de Bernoulli entre os pontos 1 e 2 do volume de controle ilustrado acima, então, temos:

p 1 ρ + v 1 2 2 + g z 1 = p 2 ρ + v 2 2 2 + g z 2

Tá legal, como ambos os pontos 1 e 2 estão expostos ao ambiente, temos p 1 = p 2 = p a t m e os termos de pressão se cancelam. Sabemos também que v 1 = V 0 e que v 2 = V 2 . Considerando o nível z 1 = 0 , então, temos z 2 = H , dessa forma, a equação de Bernoulli se torna:

V 0 2 2 = V 2 2 2 + g H → V 2 = V 0 2 - 2 g H

Então, substituindo os valores conhecidos, temos:

V 2 = 10 2 - 2 ( 9,81 ) ( 1 ) → V 2 = 8,96   m / s

Passo 2

Agora vamos aplicar a equação 4.18c apresentada nessa seção do equilíbrio de momento, para o volume de controle do passo 1:

F z = F S z + F B z = ∂ ∂ t ∫ V C   w ρ d V + ∫ S C   w ρ V → . d A →

Como o escoamento se dá em regime permanente, então a derivada no tempo será zero, e como todo o nosso volume de controle está exposto ao ambiente, não teremos força de superfície, logo F S z = 0 , dessa forma, a equação se torna:

- M g = w 1 - ρ V 0 A 1 + w 2 ( ρ V 2 A 2 )

E, nesse caso, temos w 1 = V 0 e w 2 = V 2 cos ⁡ θ , então, substituindo os valores conhecidos:

- M g = - ρ V 0 2 A 1 + V 2 cos ⁡ θ ρ V 2 A 2

No entanto, como vimos no passo 1 através da continuidade, temos V 2 A 2 = V 1 A 1 , então a equação se torna:

- M g = - ρ V 0 2 A 1 + V 2 cos ⁡ θ ρ V 1 A 1 → M g = ρ V 0 2 A 1 - V 2 cos ⁡ θ ρ V 0 A 1

M g = ρ V 0 A 1 V 0 - V 2 cos ⁡ θ → M = ρ V 0 A 1 V 0 - V 2 cos ⁡ θ g

Então, substituindo os valores conhecidos, temos:

M = 998 10 π 0,05 2 ( 10 - 8,96 cos ⁡ 30 ° ) 4 ( 9,81 ) → M = 4,47   k g

Passo 3

Mas o exercício ainda não acabou, pois queremos a massa de água, e a massa encontrada no passo 2 é a massa de água mais a do objeto, pois nosso volume de controle englobava os dois. Então, agora, para descobrir a massa de água, vamos assumir a área do jato como sendo constante, não haverão grandes perdas com essa suposição, pois a velocidade é pequena e o diâmetro da tubulação também. Dessa forma, podemos fazer:

M á g u a = ρ A 1 H = ρ π D 2 H 4

Substituindo os valores conhecidos, temos:

M á g u a = 998 π 0,05 2 1 4 → M á g u a = 1,96   k g

Resposta

M = 4,47   k g

M á g u a = 1,96   k g

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Água escoa em fluxos uniformes através de ranhuras de 2,5m m do sistema rotativo mostrado. A vazão é de 3L / s . Determine:a) O torque requerido para manter o dispositivo estacionário;b) A velocidade
Água escoa com vazão de 0,15m 3 / s através de uma tubulação com bocal que gira com velocidade constante de 30r p m . As massas do tubo inclinado e do bocal são desprezíveis comparadas com a massa de
Considere novamente o regador do Problema 4.188. Deduza uma equação diferencial para a sua velocidade angular como uma função do tempo. Avalie a velocidade de rotação em regime permanente, considerand
Petróleo bruto S G = 0,95 , proveniente de um petroleiro ancorado, escoa através de uma tubulação de 0,25m de diâmetro com a configuração mostrada. A vazão é 0,58m 3 / s e as pressões manométricas são
A figura mostra um pequeno regador de gramados. Ele opera com uma pressão manométrica de 140k P a . A vazão volumétrica total de água através dos braços do regador é de 4L / m i n . Cada jato descarre